Persamaan Garis Singgung – Pengertian, Rumus, Rujukan Soal
Rumusbilangan.com- Makalah Materi tentang Persamaan Garis Singgung – Pengertian Dan Rumus Cara Menentukannya, dan Contoh Soal Persamaan Garis Singgung.
Hallo sahabat,, hari ini kita akan membahas bahan tenatang Persamaan Garis Singgung- Pengertian Dan Rumus Cara Menentukannya.
Pada potongan ini yang akan kita bahas yakni ihwal Pengertian, Sejarah, Rumus – Rumus dan Cara menentukannya. Untuk itu, yuk pribadi saja kita mulai…

Sejarah Tentang Garis Singgung
Pada tahun 300 SM seorang ilmuan hebat matematika yang berasal dari Alexandria, Mesir yang bernama: Euklides menciptakan sejumlah rujukan garis singgung bundar dalam sebuah buku yang berjudul Elements.
Dalam karya dari Apollonius Conics (225 SM) ilmuan asala yunani, ia mendefinisikan bahwa garis singgung sebagai yang tidak ada garis lurus lain berada diantara garis itu dan kurva.
Archimedes pada sekitar tahun 287 SM menemukan sebuah garis singgung Spiral Archimedes dengan mempertimbangkan jalur – jalur perpindahan titik – titik sepanjang kurva.
Sekitar pada tahun 1630, Fermat membuatkan teknik adekualitas untuk menghitung garis singgung dan duduk perkara laiinya dalam analisa serta menghitung garis singgung parabola. Teknik ini serupa dengan mengambil perbedaan yaitu antara dan serta membaginya dengan sebuah pangkat dua dari .
Secara terpisah, Descartes menggunakan metode tegak lurus yang berdasarkan pada observasi bahwa radius bundar selalu tegak lurus dengan bundar itu sendiri.
Metode ini mengantarkan kepada pengembangan kalkulus diferensial pada sekitar periode ke – 17. Banyak orang berkontribusi di dalamnya, seperti: Roberval yang menemukan sebuah metode umum untuk menggambar garis singgung, mempertimbangkan sebuah kurva yang didefinisikan sebagai titik bergerak yang gerakannya merupakan resultan dari banyak sekali gerakan lebih sederhana.
Rene Francois de Sluse dan Johanes Hudde menemukan sebuah algoritma aljabar untuk mencari suatu garis singgung. Perkembangan lebih lanjut yaitu meliputi: John Wallis dan Isaac Newton, membawa pada teori Isaac Newton dan Gottfried Leibniz.
Definisi pada garis singgung sektar tahun 1828 ialah “garis yang benar dengan menyentuh kurva, tetapi saat diperpanjang, tidak memotong kurva tersebut”. Definisi renta ini mencegah titik belok yang mempunyai garis singgung. Definisi ini telah ditolak dan definisi modern sama dengan definisi milik Leibniz yang mendefinisikan garis singgung sebagai garis yang melalui sepasang titik tak sampai dekat kepada kurva.
Pengertian Garis Singgung
Dalam ilmu geometri, garis singgung atau biasa disebut juga garis tangen kurva bidang pada titik yang diketahui ialah garis lurus yang “hanya menyentuh” kurva pada titik tersebut.
Leibniz mendefinisikan bahwa suatu garis singgung sebagai garis yang melalui sepasang titik tak sampai bersahabat pada kurva. Lebih tepatnya, garis lurus ini disebut juga menyinggung kurva y = f (x) di titik x = c pada kurva apabila garis melalui titik (c, f (c)) pada kurva dan mempunyai kemiringan f ‘(c) dengan f ‘ ialah turunan f.
Definisi yang serupa juga dipakai pada kurva ruang dan kurva dalam ruang Euklides dimensi –n.
Karena melalui titik di mana garis singgung dan kurva bertemu, maka disebut titik singgung, garis singgung “memiliki arah yang sama” dengan kurva, dan dengan demikian merupakan pendekatan garis lurus terbaik pada kurva pada titik tersebut.
Serupa dengan garis singgung, bidang singgung permukaan pada titik yang diketahui yaitu bidang yang “hanya menyentuh” permukaan di titik tersebut. Konsep persinggungan ialah satu dari gagasan paling fundamental dalam geometri diferensial dan telah digeneralisasikan secara ekstensif.
Garis Singgung Persekutuan Luar Dua Lingkaran
Persamaan garis singgung bundar komplotan luar yaitu melibatkan dua bundar dan sebuah garis singgung lingkaran. Untuk lebih jelasnya sanggup kita lihat pada gambar di bawah berikut:
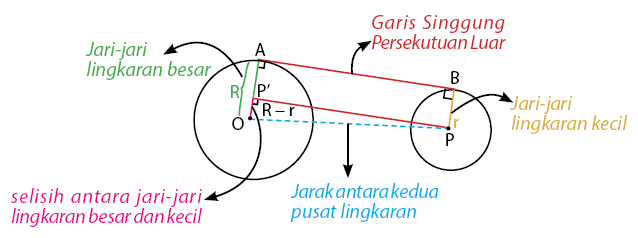
Rumus Mencari Panjang Garis Singgung Persekutuan Luar Dua Lingkaran
Rumus – rumusnya yaitu:
Keterangannya:
AB = PP’ yaitu Garis singgung komplotan luar lingkaran
OP yaitu Jarak antara kedua sentra lingkaran
R yaitu Jari-jari bundar besar
r yaitu Jari-jari bundar kecil
Garis Singgung Persekutuan Dalam Dua Lingkaran
Seperti pada garis singgung komplotan luar dua lingkaran, garis singgung komplotan dalam dua bundar ini juga melibatkan antara dua buah bundar dan sebuah garis singgung. Bedanya yaitu terletak pada posisi garis singgung lingkaran.
Dua titik singgung bundar pada garis singgung komplotan luar dua bundar terletak pada sisi yang sama. Sedangkan dua titik singgung bundar pada garis singggung komplotan dalam dua bundar terletak yang bersebrangan. Untuk lebih jelasnya, mari perhatikan gambar dibawah berikut:
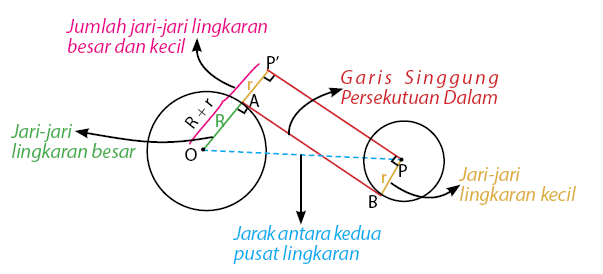
Rumus Mencari Panjang Garis Singgung Persekutuan Dalam
Rumusnya yaitu:
Keterangannya:
AB = PP’ yaitu Garis singgung komplotan luar lingkaran
OP yaitu Jarak antara kedua sentra lingkaran
R yaitu Jari-jari bundar besar
r yaitu Jari-jari bundar kecil
Contoh Soal dan Cara Menentukannya
Soal 1:
Dua buah bundar mempunyai panjang garis singgung komplotan luar 24 cm dan jarak kedua titik sentra bundar 26 cm. Apabila panjang jari-jari bundar besar 18 cm, maka panjang jari-jari bundar yang lain ialah ….
Pembahasan:
Berdasarkan data pada soal, maka kita sanggup peroleh gambar di bawah berikut:

Maka, panjang jari-jari bundar yang lain ialah 8 cm.
Soal 2:
Perhatikan gambar berikut ini:

Panjang jari-jari bundar besar dan kecil berturut-turut ialah 10 cm dan 5 cm. Jarak kedua sentra bundar tersebut yaitu 25 cm. Tentukan panjang garis singgung AB yaitu ….
Pembahasan:
Maka, panjang garis singgung AB ialah 20 cm.
Demikianlah pembahasan kita mengenai Persamaan Garis Singgung. Semoga bermanfaat ….
Baca Juga:
Cara Cepat Menentukan Persamaan Garis Singgung Lingkaran
Rumus Bola – Luas, Keliling, Volume dan Contoh Soalnya




0 Response to "Persamaan Garis Singgung – Pengertian, Rumus, Rujukan Soal"
Posting Komentar