Cara Merasionalkan Penyebut Belahan Bentuk Akar Beserta Teladan Soalnya
Berikut ini yakni pembahasan lengkap wacana menyederhanakan penyebut bagian bentuk akar, merasionalkan penyebut bentuk akar, cara merasionalkan bentuk akar, cara merasionalkan penyebut bentuk akar, cara menyederhanakan bentuk akar, merasionalkan penyebut bagian bentuk akar, pola soal merasionalkan penyebut bentuk akar.
Cara Merasionalkan Penyebut Pecahan Bentuk Akar
Pada bab sebelumnya, kau telah mempelajari bilangan rasional. Masih ingatkah kau wacana bahan tersebut? Coba kau jelaskan dengan kata-katamu sendiri.
Di dalam matematika, selain bilangan rasional, terdapat bilangan irasional.
Bilangan irasional adalah bilangan yang tidak sanggup dinyatakan dalam bentuk a/b dengan a, b bilangan lingkaran dan b ≠ 0.
Contoh bilangan irasional yakni bentuk akar, misalnya √2, √3, dan √5 . Pecahan yang penyebutnya bentuk akar juga termasuk bilangan irasional, misalnya:
Pada bab ini, kau akan mempelajari cara merasionalkan penyebut pecahan-pecahan tersebut.
Caranya yaitu dengan mengalikan pembilang dan penyebut pecahan-pecahan tersebut dengan pasangan bentuk akar sekawan penyebutnya.
Secara umum, bagian yang penyebutnya bentuk akar yang sanggup dirasionalkan adalah:
dengan a, b, dan c bilangan real. Untuk lebih jelasnya, pelajari uraian berikut.
a. Merasionalkan Benruk a/√b
Cara merasionalkan bentuk a/√b yakni dengan mengalikan pembilang dan penyebut bagian tersebut dengan bentuk sekawan dari penyebutnya, yaitu;
Contoh Soal
Rasionalkan penyebut pecahan-pecahan berikut, lalu sederhanakanlah.
b. Merasionalkan Bentuk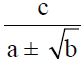 
Untuk bagian bentuk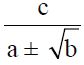
cara merasionalkannya yakni dengan mengalikan pembilang dan penyebut dengan bentuk sekawan a ± √b . Bentuk sekawan dari a + √b yakni a – √b , sedangkan bentuk sekawan dari a – √b yakni a + √b.
Contoh Soal
c. Merasionalkan Bentuk
adalah dengan mengalikan pembilang dan penyebutnya dengan bentuk sekawan dari a ± √b. Bentuk sekawan dari a + √b yakni a – √b, sedangkan bentuk sekawan dari a – √b yakni a + √b.
Contoh Soal
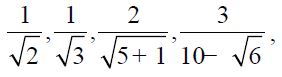
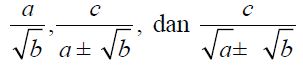
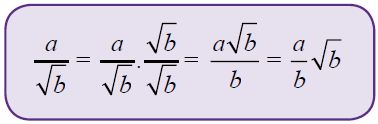
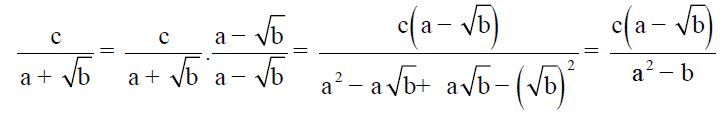
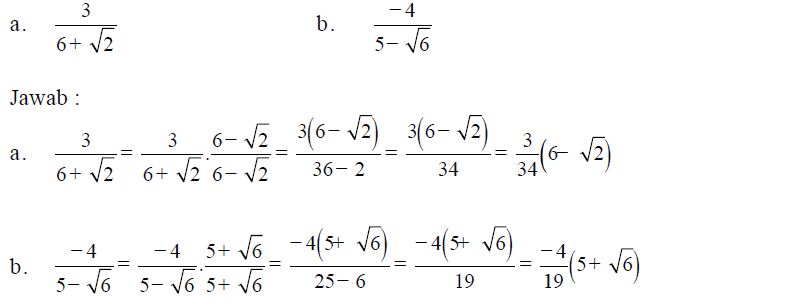
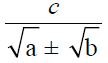
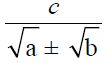
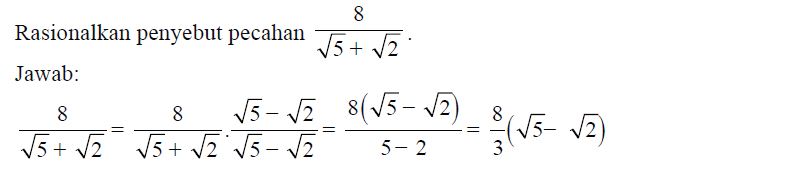
0 Response to "Cara Merasionalkan Penyebut Belahan Bentuk Akar Beserta Teladan Soalnya"
Posting Komentar