Pengertian Bilangan Berpangkat Bundar Negatif Beserta Teladan Soal Dan Pembahasannya
Berikut yakni pembahasan perihal salah satu bilangan berpangkat tak sebetulnya yaitu bilangan berpangkat negatif yang mencakup bilangan berpangkat negatif, bilangan berpangkat lingkaran negatif, pangkat lingkaran negatif, sifat sifat pangkat lingkaran negatif, pangkat negatif, pangkat nol, pangkat pecahan.
Pengertian Bilangan Berpangkat Bulat Negatif
Pada pembahasan sebelumnya telah dibahas perihal definisi bilangan berpangkat.
Bilangan berpangkat merupakan bentuk sederhana dari perkalian berulang.
Misalnya, 23 merupakan bentuk sederhana dari 2 × 2 × 2. Sekarang, bagaimana cara menguraikan 2-3 ? Untuk menjawabnya, pelajarilah uraian berikut dengan baik.
Perhatikan Sifat Bilangan Berpangkat berikut!
Untuk a bilangan real dan m, n bilangan lingkaran aktual yang memenuhi m > n, berlaku
Apa yang terjadi jikalau m < n? Jika m < n maka m – n merupakan bilangan lingkaran negatif. Pelajari pembagian bilangan berpangkat berikut.
Dari (i) dan (ii) diperoleh bahwa
Sekarang, coba kau selesaikan pembagian bilangan berpangkat berikut dengan kedua cara di atas.
Jika kau sanggup menuntaskan kedua soal tersebut dengan benar, akan memperjelas definisi bilangan berpangkat lingkaran negatif, yaitu sebagai berikut.
Dengan memakai Definisi tersebut, kau sanggup mengubah bilangan berpangkat lingkaran negatif ke dalam bilangan lingkaran aktual dan sebaliknya.
Contoh Soal Pangkat Bulat Negatif
Sifat-sifat operasi bilangan berpangkat aktual berlaku juga untuk bilangan berpangkat negatif dengan a, b bilangan real dan m, n bilangan lingkaran negatif.
Baca juga: Sifat Operasi Bilangan Berpangkat
Sumber http://www.berpendidikan.com

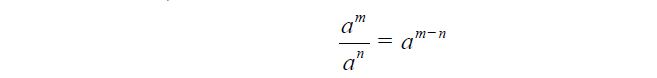
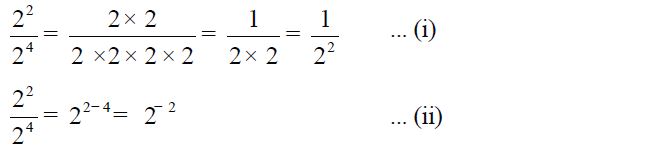




0 Response to "Pengertian Bilangan Berpangkat Bundar Negatif Beserta Teladan Soal Dan Pembahasannya"
Posting Komentar