Pengertian Dan Rumus Mencari Gradien Garis Beserta Teladan Soal Gradien
Berikut ini yaitu pembahasan perihal Gradien yang mencakup pengertian gradien, teladan soal gradien, rumus gradien, rumus gradien garis, rumus mencari gradien.
Pengertian Gradien
Pernahkah kalian melewati jalan yang naik dan turun menyerupai halnya jalan-jalan di kawasan pegunungan? Tahukah kalian bahwa dalam pembuatan jalan yang menanjak dan berkelok-kelok diharapkan perhitungan tertentu semoga kendaraan gampang melewatinya.
Salah satu perhitungan matematika yang harus diperhatikan dalam pembangunan jalan menyerupai itu yaitu kemiringannya.
Perhatikan gambar di bawah ini! Untuk menjangkau dan memadamkan titik api yang menjadi penyebab kebakaran, para petugas pemadam kebakaran memakai tangga dengan kemiringan tertentu.
Tahukah kalian mengapa tangga yang dipakai oleh pemadam kebakaran posisinya miring?
Jika kita menganggap tangga pada gambar tersebut yaitu satu garis lurus maka garis tersebut mempunyai kemiringan tertentu. Kemiringan ini dalam matematika dikenal dengan sebutan gradien.
Jadi, gradien suatu garis yaitu ukuran kemiringan atau kecondongan suatu garis.
Selain itu gradien juga disebut sebagai koefisien arah pada suatu garis lurus dan dilambangkan dengan abjad m.
Gradien adalah nilai kemiringan / kecondongan suatu garis yang membandingkan antara komponen Y (ordinat) dengan komponen X (absis).
Rumus Mencari Gradien
Ada beberapa kondisi atau keadaan untuk mencari gradien garis;
1. Gradien Garis yang Melalui Titik Pusat (0,0) dan Titik (x, y)
Kalian sudah mengetahui bahwa persamaan garis yang melalui titik sentra (0,0) dan titik (x, y) yaitu y = mx. Perhatikan teladan berikut.
Contoh Soal dan Pembahasannya
Tentukanlah gradien persamaan garis yang melalui titik sentra dan titik (3, 5)!
Penyelesaian:
Persamaan garis yang melalui titik (0, 0) dan (3, 5) yaitu y = (5/3)x. Sehingga gradiennya yaitu 5/3.
Dari teladan soal di atas sanggup disimpulkan bahwa gradien dari persaman garis y = mx yaitu m.
Kesimpulan bahwa perbandingan antara komponen y dengan komponen x pada setiap ruas garis yaitu sama. Nilai perbandingan tersebut dinamakan gradien.
Jadi, persamaan garis y = mx mempunyai gradien m dengan m = y/x.
2. Gradien Garis yang Melalui Dua Buah Titik (x1, y1) dan (x2, y2)
Tidak selamanya bahwa sebuah garis itu akan melewati titik sentra (0,0). Jika suatu garis tidak melewati titik sentra (0,0), dapatkah kalian memilih gradiennya?
Contoh Soal dan Pembahasannya
Tentukanlah gradien persamaan garis yang melalui titik (6, 2) dan titik (3, 5)!
Penyelesaian:
x1 = 6; y1 = 2; x2 = 3; y2 = 5
Jadi, gradien persamaan garisnya yaitu -1.
Kesimpulan bahwa perbandingan komponen x dan komponen y pada setiap ruas garis yaitu sama, yaitu 1. Bilangan 1 ini merupakan gradien dari persamaan garis y = x + 2.
Jadi, persaman garis y = mx, c ≠ 0 mempunyai gradien m dengan;
3. Gradien Garis Yang Sejajar Sumbu-x dan Sumbu-y
Untuk memilih gradien garis yang sejajar sumbu-x dan gradien garis yang sejajar sumbu-y kita sanggup memakai rumus;
Perhatikan gambar di bawah ini!
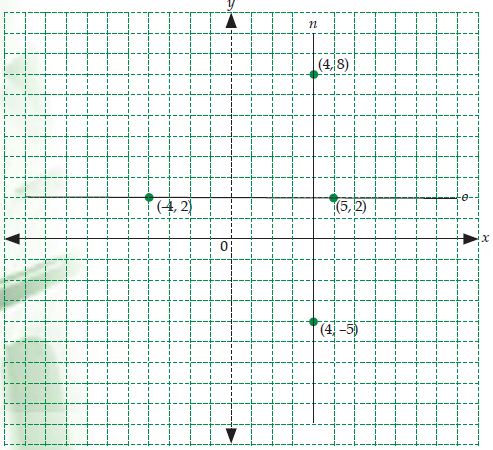
Garis o sejajar dengan sumbu-x sedangkan garis n sejajar dengan sumbu-y. Pada gambar terlihat dengan terang bahwa garis o melewati titik (-4, 2) dan (5, 2). Gradien garis o adalah
Jadi, gradien garis yang sejajar sumbu-x yaitu 0.
Perhatikan garis n di bawah ini!
Garis n melewati titik (4, 8) dan (4, -5).
Gradien garis n yaitu m = (–5 – 8):(4 – 4) = 13/0 = (tidak didefinisikan).
Jadi, gradien garis yang sejajar sumbu-y tidak didefinisikan.
4. Gradien Garis Yang Saling Sejajar
Gradien garis yang sejajar sumbu-x yaitu 0. Bagaimana dengan gradien dua buah garis yang saling sejajar menyerupai terlihat pada gambar berikut?
Perhatikan gambar di atas, kemudian lakukan aktivitas di bawah ini untuk mencari gradien garis yang saling sejajar. Apa yang sanggup kalian simpulkan menurut aktivitas tersebut?
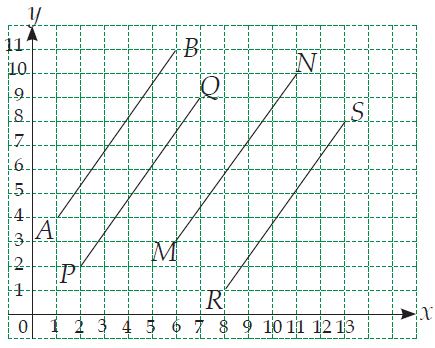
Carilah gradien ruas garis AB, PQ, MN, dan RS pada gambar di atas dengan melengkapi titik-titik berikut ini!
• Titik A (1, 4) ; B (6, 11)
Gradien AB = (11 – 4):(6 – 1) = 7/5
• Titik P (2,2) ; Q (7,9)
Gradien PQ = (9 – 2):(7 – 2) = 7/5
• Titik M (6,3); N (11,10)
Gradien MN = (10 – 3):(11–6) = 7/5
• Titik R (1,4); S (6,11)
Gradien RS = (11 – 7):(6 – 1) = 7/5
Jadi gradien garis AB = PQ = MN = RS = 7/5 .
5. Gradien Garis yang Saling Tegak Lurus
Selain kedudukan dua buah garis yang sejajar, terdapat pula kedudukan dua buah garis yang saling tegak lurus. Bagaimana gradien garis yang saling tegak lurus? Apakah gradiennya sama?
Gradien dua buah garis yang saling tegak lurus apabila dikalikan kesannya sama dengan –1. Jadi, jikalau l yaitu sebuah garis yang tegak lurus dengan garis p maka berlaku ml × mp = –1.
Perhatikan teladan berikut.
Contoh Soal dan Pembahasannya
Garis k mempunyai persamaan y = 2x + 5. Jika garis l tegak lurus garis k tentukanlah gradien garis l!
Penyelesaian:
ml = 2 ;
mk × ml = –1
ml = –(1/mk)
= –(1/2)
= –½
Jadi, gradien garis l yaitu –½.
Baca juga: Rumus Persamaan Garis Lurus
Sumber http://www.berpendidikan.com

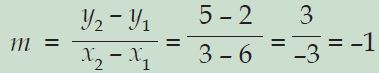
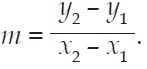
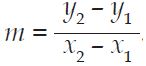
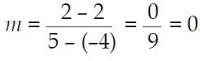
0 Response to "Pengertian Dan Rumus Mencari Gradien Garis Beserta Teladan Soal Gradien"
Posting Komentar