Contoh Soal Dan Pembahasan Barisan Dan Deret Geometri
Terlebih dahulu kita akan memahami konsep awal atau dasar-dasar dari barisan geometri yang mencakup :
Misalkan diketahui barisan menyerupai dibawah ini :
Barisan bilangan tersebut mempunyai rasio yang tetap, yaitu 3 atau r = 3. Berarti, barisan tersebut merupakan barisan geometri.
Secara umum kita sanggup menulis Barisan (Urutan) Geometrik menyerupai berikut :
dimana:
2. Untuk mencari nilai rasio(r) :
3. Mencari Suku Tengah
Kita sanggup mencari suku tengah untuk sebuah barisan geometri yang memilliki n suku ganjil (banyaknya suku harus ganjil) dimana diketahui suku pertama dan rasio, maka digunakan rumus:
Namun jikalau untuk mencari suku tengah yang kondisinya hanya diketahui suku pertama, banyaknya n suku dan suku terakhir, maka rumusnya:
Rumus suku ke n

========================= SOAL JAWAB =================================
1. Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, .....!
Dari barisan 48, 24, 12, .... didapat a = 48 dan r = 24/48 = 1/2 sehingga,
3. Dari barisan geometri diketahui bahwa U3 = 4 dan U9 = 256, maka tentukan U12!
U3 = 4 → a.r2 = 4
U9 = 256 → a.r8 = 256
Kemudian substitusikan untuk mencari U1 atau a!
→ a.r2 = 4
→ a.22 = 4
→ a = 1
Next, cari nilai U12 dengan memakai rumus umum barisan geometri!
U12 = a.rn-1
U12 = 1.211
U12 = 1.2048
U12 = 2048

5.Tentukan jumlah 10 suku pertama dari deret 32 + 16 + 8 + ….!
6. Tentukan nilai n yang memenuhi 2 + 22 + 23 + ….. + 2n = 510!
Pembahasan
U5 = 324
a = 4
Dari Un = arn −1

Dengan demikian rasionya yakni 3 atau − 3
U3 = 3
a = 12
r = 6/12 = 1/2
Un = arn −1
U5 = 12(1/2)5 −1 = 12(1/2)4 = 12(1/16) = 12/16 = 3/4
Sehingga
U3 + U5 = 3 + 3/4 = 3 3/4
Gunakan rumus umum
Sn = a(1-r^n) / (1-r)
*ket :
Sn = jumlah suku
a = suku pertama / U1
r = barisan geometri
Maka,
S5 = 16 [ 1-(3/2)^5 ] / [ 1-(3/2) ]
S5 = 16 [ 1 - (243/32) ] / -(1/2)
S5 = 16 [ (32/32) - (243/32) ] / -(1/2)
S5 = 16 ( -211/32 ) / - (1/2)
S5 = -32 ( -211/32 )
S5 = 211 cm
Maka panjang tali semula adalah 211 cm
 =
= 
 =
= 
a = 2
r = 2
n = (1 jam/ 6 menit) + 1 = 11 –> menit juga dimasukkan
Un = arn-1
U10 = 2.211-1 = 210 = 1024 buah amoeba.
Jawaban & Penjelasan:
Ini yakni bentuk barisan geometri dengan rumus suku ke n:
Un = U1.r^(n – 1) —–> ( tanda ^ berarti pangkat).
Jumlah penduduk tahun 3008 (U1) = 24 orang.
Tiap tahun penduduk bertambah 2x lipat (rasio) = 2.
Maka, jumlah penduduk tahun 3012 (U5):
Un = U1.r^(n – 1)
U5 = 24.2^(5 – 1)
U5 = 24.2^4
U5 = 24.16 = 384 orang.
Jadi, jumlah penduduk kawasan tersebut pada tahun 3012 yakni 384 orang.
19. Diketahui sebuah barisan geometri
a = 5 Un = 5120
a = 3
r = 3
n = 5
Sumber http://pusat-matematika.blogspot.com
- Apa itu barisan geometri ?
- Apa itu deret geometri ?
Apa itu Barisan Geometri ?
Barisan geometri yakni barisan yang mempunyai rasio tetap antara dua suku barisan yang berurutan. Jika dalam barisan aritmatika, selisih antara satu suku dengan suku berikutnya disebut dengan nilai beda. Sedangkan dalam barisan geometri selisih antar suku diistilahkan dengan rasio ( dilambangkan dengan r).Misalkan diketahui barisan menyerupai dibawah ini :
Barisan bilangan tersebut mempunyai rasio yang tetap, yaitu 3 atau r = 3. Berarti, barisan tersebut merupakan barisan geometri.
Secara umum kita sanggup menulis Barisan (Urutan) Geometrik menyerupai berikut :
{a, ar, ar2, ar3, ar4, ar5, ar6, ar7...}
dimana:
- a yakni suku pertama
- r yakni rasio
Rumus-Rumus Barisan Geometri
1. Untuk mencari Suku ke-n :2. Untuk mencari nilai rasio(r) :
3. Mencari Suku Tengah
Kita sanggup mencari suku tengah untuk sebuah barisan geometri yang memilliki n suku ganjil (banyaknya suku harus ganjil) dimana diketahui suku pertama dan rasio, maka digunakan rumus:
Namun jikalau untuk mencari suku tengah yang kondisinya hanya diketahui suku pertama, banyaknya n suku dan suku terakhir, maka rumusnya:
Apa itu Deret Geometri ?
Sama halnya menyerupai deret aritmatika yang merupakan jumlah dari barisan aritmatika, maka deret geometri yakni hasil penjumlahan dari nilai suku suku sebuah barisan geometri. Deret geometri dikenal juga dengan sebutan deret ukur.
Contoh:
Contoh:
- 1 + 2 + 4 + 8 +16+32
- 3 + 6 + 12 + 24 + 48 + 96
Untuk menghitung deret geometri terdapat dua rumus, yaitu :
- Rumus Deret Geometri Turun
Rumus deret geometri turun hanya sanggup digunakan jikalau 0 < r < 1
- Rumus Deret Geometri Naik
Rumus deret geometri naik hanya sanggup digunakan jikalau r > 1.
Rumus suku ke n

========================= SOAL JAWAB =================================
1. Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, .....!
Dari Barisan 3, 6, 12, ... didapat a = 3 dan r = 6/3 = 2 sehingga,
2. Tentukan Rumus Suku ke-n dari barisan 48 , 24 , 12 , ……!
- Un = a.rn-1
U7 = 3.2
U7 = 3.26
U7 = 3.64
U7 = 192
2. Tentukan Rumus Suku ke-n dari barisan 48 , 24 , 12 , ……!
Dari barisan 48, 24, 12, .... didapat a = 48 dan r = 24/48 = 1/2 sehingga,
Un = a.rn-1
Un = 48.(1/2)n-1
Un = 48.(1/2)n-1
Un = 48.(2-1)1-n
Un = 3.16.(2)1-n
U7 = 3.24(2)1-n
U7 = 3.25-n
Un = 48.(1/2)n-1
Un = 48.(1/2)n-1
Un = 48.(2-1)1-n
Un = 3.16.(2)1-n
U7 = 3.24(2)1-n
U7 = 3.25-n
U3 = 4 → a.r2 = 4
U9 = 256 → a.r8 = 256
Kemudian substitusikan untuk mencari U1 atau a!
→ a.r2 = 4
→ a.22 = 4
→ a = 1
Next, cari nilai U12 dengan memakai rumus umum barisan geometri!
U12 = a.rn-1
U12 = 1.211
U12 = 1.2048
U12 = 2048
4. Tiga buah bilangan membentuk barisan geometri. Jumlah ketiga bilangan tersebut sama dengan 35, sedangkan hasil kali ketiga bilangan itu sama dengan 1.000. Maka tentukan barisan geometri tersebut!

5.Tentukan jumlah 10 suku pertama dari deret 32 + 16 + 8 + ….!
Dari deret 32 + 16 + 8 + .... didapat a = 32 dan r = 1/2, sehingga
6. Tentukan nilai n yang memenuhi 2 + 22 + 23 + ….. + 2n = 510!
7. Diketahui suku pertama suatu deret geometri yakni 4 dengan suku ke-5 yakni 324. Tentukan rasio dari deret tersebut!
Pembahasan
U5 = 324
a = 4
Dari Un = arn −1

Dengan demikian rasionya yakni 3 atau − 3
8. Deret geometri 12 + 6 + 3 + ....Tentukan U3 + U5
Pembahasan
Pembahasan
U3 = 3
a = 12
r = 6/12 = 1/2
Un = arn −1
U5 = 12(1/2)5 −1 = 12(1/2)4 = 12(1/16) = 12/16 = 3/4
Sehingga
U3 + U5 = 3 + 3/4 = 3 3/4
9. Seutas tali dibagi menjadi 5 penggalan dengan membentuk suatu barisan geometri. Jika tali yang paling pendek yakni 16 cm dan tali yang paling panjang yakni 81 cm, maka panjang tali semula yakni ….
U1 = 16 & U5 = 81
Langkah 1 : mencari nilai rasio barisan geometri (r).Gunakan rumus umum
Un = a.r^(n-1)
*ket :
Un = nilai suku
a = suku pertama / U1
r = barisan geometri
Maka,
U5 = U1.r^(5-1)
81 = 16.r^(4)
r^(4) = 81/16
r^(4) = 3^4 / 2^4
r = 3/2
Langkah 2 : Mencari panjang total, terdapat 5 penggalan tali (S5)
Langkah 1 : mencari nilai rasio barisan geometri (r).Gunakan rumus umum
Un = a.r^(n-1)
*ket :
Un = nilai suku
a = suku pertama / U1
r = barisan geometri
Maka,
U5 = U1.r^(5-1)
81 = 16.r^(4)
r^(4) = 81/16
r^(4) = 3^4 / 2^4
r = 3/2
Langkah 2 : Mencari panjang total, terdapat 5 penggalan tali (S5)
Gunakan rumus umum
Sn = a(1-r^n) / (1-r)
*ket :
Sn = jumlah suku
a = suku pertama / U1
r = barisan geometri
Maka,
S5 = 16 [ 1-(3/2)^5 ] / [ 1-(3/2) ]
S5 = 16 [ 1 - (243/32) ] / -(1/2)
S5 = 16 [ (32/32) - (243/32) ] / -(1/2)
S5 = 16 ( -211/32 ) / - (1/2)
S5 = -32 ( -211/32 )
S5 = 211 cm
Maka panjang tali semula adalah 211 cm
10. Sebuah kendaraan beroda empat dibeli dengan haga Rp. 80.000.000,00. Setiap tahun nilai jualnya menjadi 3/4 dari harga sebelumnya. Berapa nilai jual sehabis digunakan 3 tahun ?
PEMBAHASAN :
Kata kunci dalam soal ini yakni “Setiap tahun nilai jualnya menjadi 3/4 dari harga sebelumnya”, ini artinya rasionya 3/4 dan termasuk dalam deret geometri.
Yang jadi pertanyaannya yakni suku ke-4 dengan a = 80.000.000
u4 = ar3 = 80.000.000(3/4)3 = 33.750.000
11. Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan ketinggian 3/4 kali tinggi sebelumnya, begitu seterusnya hingga bola berhenti. Jumlah seluruh lintasan bola yakni …
PEMBAHASAN :
Karena bola memantul terus-terusan hingga berhenti, berarti ini termasuk deret geometri tak hingga. Untuk mencari panjang lintasan bola yang memantul ini, rumus yang digunakan adalah
Panjang lintasan = ketinggian bola jatuh + 2(kali deret takhingga)
Dalam deret takhingga ini, yang menjadi suku pertamaya yakni pantulan pertama (bukan ketinggian bola jatuh pada awal).
Pantulan pertama = 10 x 3/4 = 30/4 m (suku pertama)
= 
= 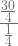 = 30
= 30
P.Lintasan = 10 + 2(30) = 70m
12. Jumlah deret geometri tak hingga yakni 7, sedangkan jumlah suku – suku yang bernomor genap yakni 3. Suku pertama deret tersebut yakni … PEMBAHASAN :
Deret geometri : a + ar + ar2 + ar3 + ar4 + ar5 + ar6 + …
Perhatikan suku genap dan ganjilnya, dimana pada suku-suku genap, suku pertamanya yakni ar dan pada suku-suku ganjil, suku pertamanya yakni ar, dengan rasionya yakni r2.
7 = 
7(1 – r) = a … (i)
Berdasarkan rumus jumlah deret geometri tak hingga diatas, maka kita memperoleh rumus deret geometri takhingga bersuku genap dengan mengganti suku awal dengan “ar” dan rasionya “r2“.
Sgenap = 
3 = 
3(1 – r2) = ar … (ii)
Substitusi (i) ke (ii), sehingga diperoleh :
3(1 – r2) = (7(1 – r))r
3 – 3r2 = 7r – 7r2
4r2 – 7r + 3 = 0
(4r-3)(r-1) = 0
r = 3/4 atau r = 1
substitusi nilai “r” tersebut ke persamaan (i), sehingga diperoleh :
untuk r = ¾
a = 7(1 – r) = 7(1 – 3/4) = 7/4
untuk r = 1
a = 7(1 – r) = 7(1 – 1) = 0
13. Pertambahan penduduk suatu kota tiap tahun mengikuti hukum barisan geometri. Pada tahun 1996 pertambahannya sebanyak 6 orang, tahun 1998 sebanyak 54 orang. Pertambahan penduduk pada tahun 2001 yakni … orang.
PEMBAHASAN :
tahun 1996 => u1 = a = 6
tahun 1998 => u3 = ar2 = 54
6.r2 = 54
r2 = 9 => r = 3
tahun 2001 => u6 = ar5
6.(3)5 = 1.458
14. Diketahui barisan geometri dengan
u1 = x3/4 dan u4 = x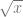 . Rasio barisan geometri tesebut yakni …
. Rasio barisan geometri tesebut yakni …

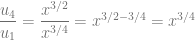

u1 = x3/4 dan u4 = x
PEMBAHASAN :
15. Sebuah amoeba sanggup membelah diri menjadi 2 setiap 6 menit. Pertanyaannya, berapakah jumlah amoeba sehabis satu jam jikalau pada awalnya terdapat 2 amoeba?
a = 2
r = 2
n = (1 jam/ 6 menit) + 1 = 11 –> menit juga dimasukkan
Un = arn-1
U10 = 2.211-1 = 210 = 1024 buah amoeba.
16. Diketahui sebuah barisan geometri a, b, c,…. Jika diketahui a x b x c = 1728 dan a + b + c = 36, maka nilai a, b dan c adalah…
Jawaban & Penjelasan:
Penyelesaian:
a x b x c = 1728 <—–> a.c = 1728/b
a + b + c = 36 <—–> a + c = 36 – b
Rasio = U2/U1 = U3/U2
b/a = c/b
b² = ac —–> kali silang
b² – ac = 0
b² – 1728/b = 0
b³ – 1728 = 0
b³ = 1728
b = ³√1728 = 12.
Subtitusi nilai b.
a.c = 1728/b = 1728 /12 = 144.
a + c = 36 – b = 36 – 12 = 24.
Nilai a dan c yang paling memungkinkan jikalau nilai a.c = 144 dan a + c = 24 yakni a dan c = 12. Sebab,
12.12 = 144 dan 12 + 12 = 24.
Jadi nilai a, b dan c yakni 12, 12, 12. Rasionya = 1.
Pembahasan & Jawaban:
Untuk mencari suku ke-n, jikalau diketahui jumlah nilai suku-sukunya, maka rumus yang berlaku adalah:
Un = Sn – S(n – 1)
Jumlah nilai 9 suku pertama
Sn = 2n² + 4n
S9 = 2(9)² + 4(9)
S9 = 2.81 + 36
S9 = 198.
Jumlah nilai 8 suku pertama
Sn = 2n² + 4n
S8 = 2(8)² + 4(8)
S8 = 2.64 + 32
S8 = 160.
Maka nilai dari suku ke-9 adalah
Un = Sn – S(n – 1)
U9 = S9 – S8
U9 = 198 – 160 = 38.
Penyelesaian:
a x b x c = 1728 <—–> a.c = 1728/b
a + b + c = 36 <—–> a + c = 36 – b
Rasio = U2/U1 = U3/U2
b/a = c/b
b² = ac —–> kali silang
b² – ac = 0
b² – 1728/b = 0
b³ – 1728 = 0
b³ = 1728
b = ³√1728 = 12.
Subtitusi nilai b.
a.c = 1728/b = 1728 /12 = 144.
a + c = 36 – b = 36 – 12 = 24.
Nilai a dan c yang paling memungkinkan jikalau nilai a.c = 144 dan a + c = 24 yakni a dan c = 12. Sebab,
12.12 = 144 dan 12 + 12 = 24.
Jadi nilai a, b dan c yakni 12, 12, 12. Rasionya = 1.
17. Pada sebuah deret geometri, rumus jumlah suku ke-n nya yakni Sn = 2n² + 4n. Tentukan nilai suku ke-9 dari deret tersebut?
Pembahasan & Jawaban:
Untuk mencari suku ke-n, jikalau diketahui jumlah nilai suku-sukunya, maka rumus yang berlaku adalah:
Un = Sn – S(n – 1)
Jumlah nilai 9 suku pertama
Sn = 2n² + 4n
S9 = 2(9)² + 4(9)
S9 = 2.81 + 36
S9 = 198.
Jumlah nilai 8 suku pertama
Sn = 2n² + 4n
S8 = 2(8)² + 4(8)
S8 = 2.64 + 32
S8 = 160.
Maka nilai dari suku ke-9 adalah
Un = Sn – S(n – 1)
U9 = S9 – S8
U9 = 198 – 160 = 38.
18. Sebuah kawasan pada tahun 3008 mempunyai jumlah penduduk 24 orang. Tiap tahunnya jumlah penduduk bertambah dua kali lipatnya. Maka, jumlah penduduk pada tahun 3012 adalah…
Jawaban & Penjelasan:
Ini yakni bentuk barisan geometri dengan rumus suku ke n:
Un = U1.r^(n – 1) —–> ( tanda ^ berarti pangkat).
Jumlah penduduk tahun 3008 (U1) = 24 orang.
Tiap tahun penduduk bertambah 2x lipat (rasio) = 2.
Maka, jumlah penduduk tahun 3012 (U5):
Un = U1.r^(n – 1)
U5 = 24.2^(5 – 1)
U5 = 24.2^4
U5 = 24.16 = 384 orang.
Jadi, jumlah penduduk kawasan tersebut pada tahun 3012 yakni 384 orang.
19. Diketahui sebuah barisan geometri
4p, 2q, r, … . Maka nilai dari q² – pr adalah…
Jawaban & Penjelasan:
Penentuan rasio.
r = U2/U1 = U3/U2
2q/4p = r/2q
2q.2q =4p.r —–> kali silang
4q² = 4pr
4q² – 4pr = 0
4(q² -pr) = 0
q² -pr = 0
Jawaban & Penjelasan:
Penentuan rasio.
r = U2/U1 = U3/U2
2q/4p = r/2q
2q.2q =4p.r —–> kali silang
4q² = 4pr
4q² – 4pr = 0
4(q² -pr) = 0
q² -pr = 0
20.Diketahui sebuah barisan geometri :
5, 10, 20, 40, 80, .... , 5120.
Nilai suku tengahnya yakni :
a = 5 Un = 5120
Ut = √a . Un
Ut = √5 . 5120 = √25600 = 160
21. Terdapat sebuah barisan geometri sebanyak lima suku. Jika suku pertamanya yakni 3 dan rasionya yakni 3. Berapakah suku tengahnya ?
r = 3
n = 5
Ut = √a . rn = √3 . 35=729 = 27




0 Response to "Contoh Soal Dan Pembahasan Barisan Dan Deret Geometri"
Posting Komentar