Kesebangunan Dan Kekongruenan Bangkit Datar Segitiga Dan Trapesium
Kesebangunan Dan Kekongruenan Bangun Datar Segitiga Dan Trapesium – Hallo sahabat, pada pecahan kali ini, kita akan membahas bahan yang sering muncul dalam kisi-kisi ujian nasional, yaitu: wacana kesebangunan dan kekongruenan yang mencakup wacana pengertian dan referensi – contohnya.
Mari kita ulas, kesebangunan dan kekongruenan yakni merupakan salah satu pecahan dari ilmu geometri. Materi ini mencakup kesebangunan dan kekongruenan bangkit datar segitiga dan trapesium. Materi ini sangat cocok bagi mitra – mitra yang akan menghadapi ujian nanti, alasannya bahan yang akan kita pelajari ini, yakni bahan yang sering muncul dalam kisi – kisi ujian nasional.
Pengertian Kesebangunan
Kesebangunan yakni suatu bangkit datar yang mana sudut – sudutnya mempunyai kesesuaian yang sama besarnya serta panjang sisi – sisi sudutnya bersesuai yang mempunyai sebuah perbandingan yang sama.
Dengan kata lain, kesebangunan yakni dua buah bangkit yang mempunyai sudut dan panjang sisi yang sama.
Kesebangunan dilambangkan dengan simbol notasi ≈.
Lihat referensi berikut:
Dua Bangun Datar Yang Sebangun
Bangun datar ini sebangun dengan: 
Dua bangkit datar diatas merupakan dua bangkit yang sebangun, dengan beberapa sifat – sifat sebagai berikut:
1. Pasangan Sisi -Sisinya Yang Bersesuaian Memiliki Perbandingan Nilai Yang Sama. Berikut Uraiannya:
- Sisi AD dan KN adalah
- Sisi AB dan KL adalah
- Sisi BC dan LM adalah
- Sisi CD dan MN adalah
Maka, dapat disimpulkan yaitu : 
2. Besar Sudut Yang Bersesuaian yakni Sama, yaitu;
Dua Bangun Segitiga Yang Sebangun
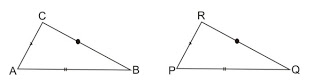
Perhatikan gambar segitiga berikut:
Bangun segitiga ABC ini sebangun dengan bangkit segitiga PQR yakni: 
Dari dua gambar di atas, untuk menandakan bahwa gambar tersebut yakni sebangun, mdapat kita lihat dengan menguraikan beberapa sifat – sifatnya, yaitu:
1. Perbandingan Antara Sisinya Sama Besar dan Bersesuaian Sama Besar, yaitu:
AC bersesuaian dengan PR yakni: 
AB bersesuaian dengan PQ yakni : 
BC bersesuaian dengan QR yakni: 
Sehingga, dapat disimpulkan bahwa : 
2. Besar Sudut – Sudut Yang Bersesuaian Sama, yaitu:
Pengertian Kekongruenan
Kekongruenan yakni dua buah bangkit datar yang keduanya sama – sama mempunyai bentuk dan ukuran yang sama. Kekongruenan ini di lambangkan dengan simbol ≅.
Perhatikan referensi berikut:
1. Dua Bangun Datar yang Kongruen
Pada kedua bangkit di atas yakni bangkit yang kongruen, alasannya panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh alasannya itu, pada bangun KLMN dan PQRS dapat dikatakan yakni kongruen alasannya mempunyai bentuk dan ukuran yang sama.
2. Dua Segitiga Yang Kongruen
Secara geometris dua segitiga yang kongruen ialah dua segitiga yang saling menutupi dengan tepat. Sifat dua segitiga kongruen tersebut, yaitu:
a. Pasangan sisi yang bersesuaian yakni sama panjang
b. Sudut yang bersesuaian adalahsama besar
Segitiga sanggup dikatakan kongruen mana kala sanggup memenuhi syarat yskni sebagai berikut:
a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)
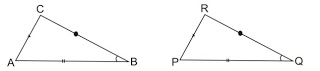
Berdasarkan gambar segitiga ABC dan segitiga PQR di atas, bahwa keduanya mempunyai panjang AB = PQ, panjang AC = PR, dan panjang BC = QR.
b. Sudut dan Dua Sisi Yang Bersesuaian Sama Besar (sisi, sudut, sisi)
Berdasarkan bangkit segitiga ABC dan segitiga PQR di atas, bahwa keduanya mempunyai sisi AB = PQ, ∠B = ∠Q, dan sisi BC = QR
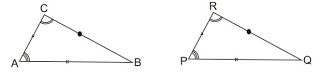
c. Satu Sisi Apit dan Dua Sudut Yang Bersesuaian Sama Besar (sudut, sisi, sudut)
Berdasarkan bangkit segitiga ABC dan segitiga PQR di atas bahwa, ∠A = ∠P, sisi AC = PR, dan ∠Q = ∠R
Contoh Soal Dan Pembahasan
Soal 1:
Beno mempunyai tinggi tubuh 150 cm. Dia berdiri pada titik yang berjarak 10 m dari sebuah gedung. Ujung bayangan Beno berimpit dengan ujung bayangan gedung. Apabila panjang bayangan Febri yakni 4 m, maka tinggi gedung itu yakni ….
Pembahasan
Kita perhatikan terlebih dahulu bangkit segitiga ABE dan segitiga ACD!
Berdasarkan prinsip kesebangunan, maka sanggup kita peroleh 
Sehingga:
Hasilnya yaitu: DC = 5,24 m
Soal 2:
Perhatikan gambar bangkit datar berikut:
Berdasarkan bangkit persegi panjang ABCD dan PQRS di atas yakni sebagun. Maka tentukanlah:
a. Berapa panjang PQ?
b. Berapa luas dan keliling persegi panjang PQRS?
Pembahasan:
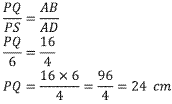
a. Perbandingan sisi AB dengan AD bersesuaian dengan sisi PQ dan PS sehingga:
Maka: panjang PQ yakni 24
b. Mencari luas dan keliling persegi panjang PQRS:
Luas persegi panjang yakni panjang x lebar
Luas persegi panjang PQRS yaitu: PQ x PS = 24 cm x 6 cm = 144 cm2
Keliling persegi panjangnya yaitu:
Keliling persegi panjang PQRS = PQ + QR + RS + SP = 24 cm + 6 cm + 24 cm + 6 cm = 60 cm
Demikianlah pembahasana bahan mengenai kesebangunan dan kekongruean. Semoga sanggup memperlihatkan manfaat …
Baca Juga:
Sumber aciknadzirah.blogspot.com
0 Response to "Kesebangunan Dan Kekongruenan Bangkit Datar Segitiga Dan Trapesium"
Posting Komentar