Rumus Phytagoras – Dalil Teorema Pythagoras Dan Teladan Soal
Dalil Pythagoras | Dalil phytagoras sering dikenal dengan istilah Teorema phytagoras (pitagoras). Kalimat pythagoras niscaya sudah tidak gila lagi di indera pendengaran kita, sebab semenjak SD dikala pembelajaran matematika niscaya kita tidak ketinggalan untuk mempelajari pytagoras. Rumus phytagoras merupakan rumus yang ditemukan oleh ilmuwan yunani yang bernama pythagoras.
Pengertian dari teorema pythagoras atau dalil phytagoras yaitu berbunyi :
Sisi miring atau sisi terpanjang dalam segitiga siku – siku sama dengan kuadrat sisi – sisi lainnya.
Perhatikan gambar di bawah ini :
Segitiga di atas merupakan segitiga siku-siku yang mempunyai satu sisi tegak (BC), satu sisi mendatar (AB), dan satu sisi miring (AC).
Dalil pythagoras atau rumus pythagoras berfungsi untuk mencari salah satu sisi dengan kedua sisi diketahui.
Rumus Phytagoras (Pythagoras) :
b2 = a2 + c2
Maka untuk menghitung sisi tegak dan sisi mendatarnya berlaku rumus :
a2 = b2 – c2
c2 = b2 – a2
Rumus Pythagoras dalam bentuk akar
- Jika sisi miringnya c
- Sisi tegak dan mendatarnya yaitu a dan b
Maka rumus pitagoras yang dihasilkan :
Catatan Penting : Rumus pythagoras, hanya berlaku pada segitiga siku – siku saja.
Teorema Phytagotas
Dalam dalil /teorema pythagoras, ada pola angka yang perlu untuk diingat supaya dalam menuntaskan soal pythagoras akan lebih gampang dan cepat dalam mengerjakannya, pola tersebut yaitu :
- 3 – 4 – 5
- 5 – 12 – 13
- 6 – 8 – 10
- 7 – 24 – 25
- 8 – 15 – 17
- 9 – 12 – 15
- 10 – 24 – 26
- 12 – 16 – 20
- 14 – 48 – 50
- 15 – 20 – 25
- 15 – 36 – 39
- 16 – 30 – 34
Untuk memahami lebih jelasnya mengenai dalil phytagoras, maka perhatikan pola sebagai berikut
Contoh Soal Phytagoras dan Pembahasannya
Contoh Soal 1
- Suatu segitiga siku- siku mempunyai sisi tegak (AB) panjangnya 15 cm ,dan sisi mendatarnya (BC) 8 cm, berapakah cm kah sisi miringnya (AC) ?
Penyelesaian :
Diketahui :
AB = 15
BC = 8
Ditanya : Panjang AC …???
Jawab :
Cara pertama :
AC2 = AB2 + BC2
AC2 = 152 + 82
AC2 = 225 + 64
AC2 = 289
AC = √289
AC = 17
Cara Kedua :
AC = √ AB2 + BC2
AC = √ 152 + 82
AC = √ 255 + 64
AC = √ 289
AC = 17
Jadi, panjang AC yaitu 17 cm
Contoh Soal 2
- Berapakah panjang sisi tegak suatu segitiga siku – siku apabila diketahui panjang sisi miringnya 13 cm dan sisi datarnya 5 cm ?
Penyelesaiaannya :
Misal : c = sisi miring , b = sisi datar , a = sisi tegak
Diketahui : c = 13 cm , b = 5 cm
Ditanya : a = ….????
Jawab :
Cara Pertama :
a2 = c2 – b2
a2 = 132 – 52
a2 = 169 – 25
a2 = 144
a = √ 144
a = 12
Cara Kedua :
a = √ c2 – b2
a = √ 132 – 52
a = √ 169 – 25
a = √ 144
a = 12
Jadi, panjang sisi tegak segitiga tersebut yaitu 12 cm
Contoh Soal 3
- Ada sbuah segitiga ABC, siku – siku di B. Apabila panjang AB = 16 cm dan BC = 30, Maka berapakah panjang sisi miring segitiga tersebut ( AC ) ?
Penyelesaian :
Diketahui :
AB = 16
BC = 30
Ditanya : AC = . . . ?
Jawab :
AC = √ AB2 + BC2
AC = √ 16 2 + 302
AC = √ 256 + 900
AC = √ 1156
AC = 34
Jadi , panjang AC = 34 cm
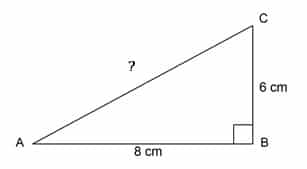
Contoh Soal 4
4. Perhatikan gambar dibawah ini, iketahui Segitiga Siku-Siku ABC Memiliki nilai sisi tegak 6 cm dan sisi bantalan 8 cm, Hitunglah berapa panjang sisi miringnya ?
Penyelesaian :
Diketahui :
- AB = 8 cm
- BC = 6 cm
Ditanya : Panjang AC (Sisi Miring Segitiga Siku-Siku Diatas) ….?
Jawab :
AC2 = AB2 + BC2
AC2 = 82 + 62
AC2 = 64 + 36
AC2 = 100
AC = √100
AC = 10
Itulah beberapa pola soal phytagoras dan pembahasannya beserta jawabannya.
Untuk lebih memahami silahkan anda kerjakan beberapa soal latihan berguru phytagoras dibawah ini.
Latihan Soal Phytagoras
1. Ada sebuah segitiga PQR XYZ diketahui sisi-sisinya diantaranya x, y, dan z. Dari pernyataan berikut ini yang benar yaitu ….?
A. jikalau y² = x² + z² , < X = 90º
B. jikalau z² = y² – x² , < Z = 90º
C. jikalau z² = x² – y² , < Y = 90º
D. jikalau x² = y² + z² , < X = 90º
A. 9 cm
B. 15 cm
C. 25 cm
D. 68 cm3. Ada sebuah segitiga yang siku-siku, hipotenusanya 4 √3 cm dan salah satu sisi siku-sikunya ialah 2 √2 cm. Berapakah, Panjang sisi siku-siku lain …. cm
A. 2 √10
B. 3 √5
C. 8 √2
D. 3 √3
4. Panjang hepotenusa segitiga yang siku-siku sama kaki ialah 16 cm dan panjang kaki-kakinya yaitu x cm. Hitunglah nilai x …. cm
A. 4 √2
B. 4 √3
C. 8 √2
D. 8 √3
Demikian klarifikasi perihal dalil pythagoras , supaya bermanfaat dan dapat membantu dalam berguru matematika yang sering menciptakan sebagian dari kita pusing tujuh keliling, padahal aslinya jikalau kita mempelajari dengan tekun maka semua hal yang sulit akan menjadi mudah.
Inti dari rumus dalil pythagoras yaitu sisi miring sama dengan sisi tegak di tambah sisi mendatar ( akan tetapi jangan lupa untuk dikuadratkan ). Good luck
Sumber http://b1ixbux.com
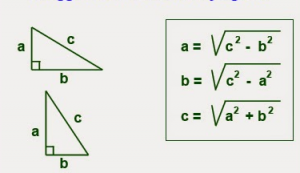
0 Response to "Rumus Phytagoras – Dalil Teorema Pythagoras Dan Teladan Soal"
Posting Komentar