Pengertian, Teladan Dan Rumus Barisan Geomateri Beserta Teladan Soal Barisan Geometri
Berikut ini yaitu pembahasan ihwal barisan geometri yang mencakup pengertian barisan geometri, rujukan barisan geometri, rumus barisan geometri, rujukan soal barisan geometri, macam macam barisan geometri, jenis jenis barisan geometri.
Pengertian Barisan Geometri
Berdasarkan polanya, barisan bilangan dibagi menjadi dua bagian, yaitu barisan arimetika (barisan hitung) dan barisan geometri (barisan ukur). Agar kau lebih memahaminya, perhatikan uraian berikut ini.
Barisan geometri adalah barisan bilangan yang mempunyai rasio tetap antara dua suku barisan yang berurutan.
Berbeda dengan barisan aritmetika, selisih antarsuku barisan disebut rasio (dilambangkan dengan r). Artinya, suku barisan ditentukan oleh perkalian atau pembagian oleh suatu bilangan tetap dari suku barisan sebelumnya.
Pelajari uraian berikut.
- Diketahui barisan bilangan sebagai berikut.
Barisan bilangan tersebut mempunyai rasio yang tetap, yaitu 2 atau r = 2. Berarti, barisan tersebut merupakan barisan geometri.
- Diketahui barisan bilangan sebagai berikut.
Barisan bilangan tersebut mempunyai rasio yang tetap, yaitu Berarti, bilangan tersebut merupakan barisan geometri.
Uraian tersebut memperjelas bahwa barisan geometri mempunyai rasio tetap.
Jika r bernilai lebih besar dari 1, barisan geometri tersebut merupakan barisan geometri naik. Adapun kalau r lebih kecil dari 1, barisan geometri tersebut merupakan barisan geometri turun.
Contoh Soal Barisan Geometri
Tentukan apakah barisan bilangan geometri berikut merupakan barisan geometri naik atau turun.
Rumus Barisan Geometri
Sekarang, coba kau perhatikan barisan bilangan geometri berikut.
- U1, U2, U3, U5, U6, …, Un – 1, Un
Dari barisan tersebut diperoleh
- U1 = a
- U2 = U1 × = a × r = ar
- U3 = U2 × r = (a × r) × r = ar2
- U4 = U3 × r = (a × r2) × r = ar3
- U5 = U4 × r = (a × r3) × r = ar4
- U6 = U5 × r = (a × r4) × r = ar5
- …
- Un =Un–1 ×r = (a × rn-2) × r =arn-1
Jadi, untuk mencari suku ke-n barisan geometri dipakai rumus sebagai berikut.
Untuk mencari rasio dalam suatu barisan geometri, perhatikan uraian berikut.
Jadi, rasio pada barisan geometri sanggup dinyatakan sebagai berikut.




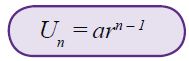
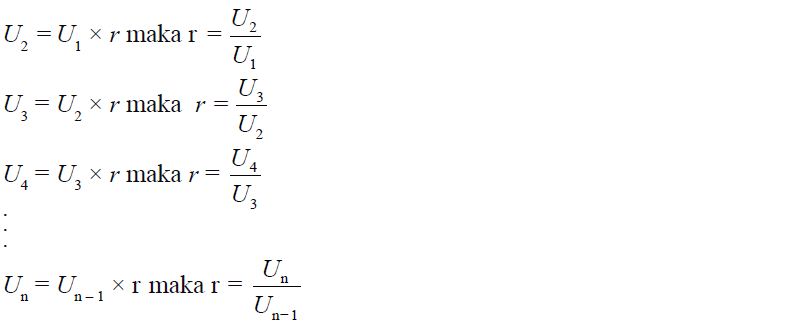




0 Response to "Pengertian, Teladan Dan Rumus Barisan Geomateri Beserta Teladan Soal Barisan Geometri"
Posting Komentar