Pengertian, Tumpuan Dan Rumus Barisan Aritmatika Beserta Tumpuan Soal Barisan Aritmatika
Berikut ini ialah pembahasan wacana barisan aritmatika yang mencakup pengertian barisan aritmatika, pola barisan aritmatika, rumus barisan aritmatika, pola soal barisan aritmatika.
Pengertian Barisan Aritmatika
Berdasarkan polanya, barisan bilangan dibagi menjadi dua bagian, yaitu barisan arimetika (barisan hitung) dan barisan geometri (barisan ukur). Agar kau lebih memahaminya, perhatikan uraian berikut ini.
Barisan aritmetika adalah barisan bilangan yang mempunyai beda atau selisih yang tetap antara dua suku barisan yang berurutan.
Perhatikan uraian berikut.
- Diketahui barisan bilangan:
Barisan bilangan tersebut mempunyai beda atau selisih 3 antara dua suku barisan yang berurutan. Berarti, barisan bilangan tersebut merupakan barisan aritmetika.
- Diketahui barisan bilangan:
Barisan bilangan tersebut mempunyai beda atau selisih yang tetap antara dua suku barisan yang berurutan, yaitu –4. Berarti, barisan bilangan tersebut merupakan barisan aritmetika.
Dari kedua uraian tersebut, sanggup disimpulkan bahwa barisan aritmetika mempunyai beda (sering dilambangkan dengan b) yang tetap.
Jika b bernilai positif maka barisan aritmetika itu dikatakan barisan aritmetika naik. Sebaliknya, Jika b bernilai negatif maka barisan aritmetika itu disebut barisan arimetika turun.
Untuk lebih jelasnya, perhatikan pola soal berikut.
Contoh Soal Barisan Aritmatika
Tentukan jenis barisan aritmetika berikut menurut nilai bedanya.
a. 30, 32, 34, 36, 38, …
b. 18, 15, 12, 9, 6, 3, …
c. −10, −14, –18, −22, −26, …
Jawab
Rumus Barisan Aritmatika
Kamu telah memahami barisan aritmetika naik dan turun. Sekarang, bagaimana mencari salah satu suku barisan jikalau yang diketahui hanya suku pertama dan bedanya saja?
Bagaimana mencari beda jikalau yang diketahui hanya suku pertama dan satu suku barisan yang lain? Untuk menjawabnya, pelajarilah uraian berikut.
Diketahui barisan bilangan aritmetika sebagai berikut.
- U1, U2, U3, U4, U5, U6, …, Un – 1 , Un
Dari barisan tersebut diperoleh
- U1 = a (suku pertama dilambangkan dengan a)
- U2 = U1 + b = a + b
- U3 = U2 + b = (a + b) + b = a + 2b
- U4 = U3 + b = (a + 2b) + b = a + 3b
- U5 = U4 + b = (a + 3b) + b = a + 4b
- U6 = U5 + b = (a + 4b) + b = a + 5b
- …
- Un = Un − 1 + b = (a + (n − 2) b ) + b = a + (n − 1) b
Jadi, rumus ke-n barisan aritmetika sanggup ditulis sebagai berikut.
Untuk mencari beda dalam suatu barisan aritmetika, coba kau perhatikan uraian berikut.
- U2 = U1 + b maka b = U2 − U1
- U3 = U2 + b maka b = U3 − U2
- U4 = U3 + b maka b = U4 − U3
- U5 = U4 + b maka b = U5 − U4
- …
- Un = Un − 1 + b maka b = Un − Un − 1
Jadi, beda suatu barisan aritmetika dinyatakan sebagai berikut.
Agar kau lebih memahami bahan ini, perhatikan contoh-contoh soal berikut.
Contoh Soal Barisan Arimatika
Diketahui barisan aritmetika sebagai berikut.
10, 13, 16, 19, 22, 25, ….
Tentukan:
a. jenis barisan aritmetikanya,
b. suku kedua belas barisan tersebut.
Jawab:
a. Untuk memilih jenis barisan aritmetika, tentukan nilai beda pada barisan tersebut.
b = U2 − U1
= 13 − 10
= 3
Oleh alasannya ialah b > 0, barisan aritmetika tersebut merupakan barisan aritmetika naik.
b. Untuk mencari suku kedua belas (U12), dilakukan cara sebagai berikut.
Un = a + (n − 1)b maka
U12 = 10 + (12 − 1) 3
= 10 + 11 · 3
= 10 + 33
= 43
Jadi, suku kedua belas barisan tersebut ialah 43.
Sebuah barisan aritmetika mempunyai suku pertama 6 dan suku ketujuh 24.
a. Tentukan beda pada barisan tersebut.
b. Tuliskan sepuluh suku pertama dari barisan tersebut.
Jawab:
Diketahui :
suku pertama = a = 6
suku ketujuh = U7 = 36
a. Untuk memilih beda:
Un = a + (n − 1) b maka
U7 = 6 + (7 − 1) b
36 = 6 + 6 b
36 − 6 = 6 b
30 = 6 b
b = 5
Jadi, beda pada barisan itu ialah 5.
b. Dengan suku pertama 6 dan beda 5 diperoleh barisan aritmetika sebagai berikut.
6, 11, 16, 21, 26, 31, 36, 41, 46, 51
Diketahui suatu barisan aritmetika :−8, −3, 2, 7, 12, 17, …
Tentukan rumus suku ke-n yang berlaku pada barisan tersebut.
Jawab:
Diketahui:
a = U1 = −8
b = U2 − U1
= −3 − (−8)
= −3 + 8
= 5
Jadi, rumus umum yang berlaku pada barisan tersebut adalah
Un = a + (n − 1) b
= −8 + (n − 1) 5
= −8 + 5n − 5
= 5n − 13
Setiap bulan, Ucok selalu menabung di bank. Pada bulan pertama, beliau menabung sebesar Rp10.000,00, bulan kedua beliau menabung sebesar Rp11.000,00, bulan ketiga beliau menabung sebesar Rp12.000, 00. Demikian seterusnya, beliau selalu menabung lebih Rp1.000,00 setiap bulannya.
a. Nyatakanlah uang yang ditabung Ucok (dalam ribuan rupiah) untuk 8 bulan pertama.
b. Tentukan jumlah uang yang ditabung Ucok pada bulan ke-12.
Jawab :
a. Dalam ribuan rupiah, uang yang ditabung Ucok untuk 8 bulan pertama ialah sebagai berikut.
10, 11, 12, 13, 14, 15, 16, 17
b. Diketahui : U1 = 10
b = 1
U12 = a + (n – 1) b
= 10 + (12 – 1) 1
= 10 + 11
= 21
Jadi, uang yang ditabung Ucok pada bulan ke-12 ialah Rp21.000,00.
Di dalam suatu gedung pertunjukan, disusun dingklik dengan baris paling depan terdiri atas 12 kursi, baris kedua 14 kursi, baris ketiga 16 kursi, dan seterusnya selalu bertambah dua. Banyak dingklik pada baris ke- 20 ialah ….
Jawab:
Misalkan, Un = banyak dingklik pada baris ke-n
Diketahui:
U1 = 12,
U2 = 14, dan
U3 = 16
Ditanyakan: U20?
Penyelesaian:
Banyak dingklik pada setiap baris membentuk barisan aritmetika dengan a = 12 dan b = 2.
Jadi, Un = a + (n –1)b
U20 = 12 + (20 – 1)2
= 12 + (19)2
= 12 + 38
= 50
Baca juga: Pengertian Barisan Bilangan
Sumber http://www.berpendidikan.com



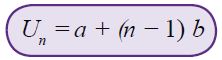
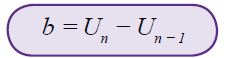
0 Response to "Pengertian, Tumpuan Dan Rumus Barisan Aritmatika Beserta Tumpuan Soal Barisan Aritmatika"
Posting Komentar