Definisi Atau Pengertian Pemetaan (Fungsi) Dalam Matematika Beserta Cara Penyajiannya
Berikut ini merupakan pembahasan wacana pemetaan atau fungsi yang mencakup pengertian pemetaan, pengertian fungsi, penyajian pemetaan, pengertian fungsi berdasarkan para ahli, pengertian perpetaan, pengertian fungsi matematika, definisi pemetaan, pengertian fungsi dalam matematika.
Konsep pemetaan atau fungsi mempunyai keterkaitan dengan konsep korelasi yang dibahas pada bab sebelumnya. Apa yang dinamakan fungsi dan bagaimana menyajikannya, marilah kita pelajari pada pembahasan berikut!
Pengertian Pemetaan atau Fungsi
Banyak referensi yang mengatakan hubungan atau relasi antara satu objek dengan objek lainnya.
Misalnya korelasi antara nama negara dan ibukotanya menyerupai terlihat pada diagram panah di bawah ini.
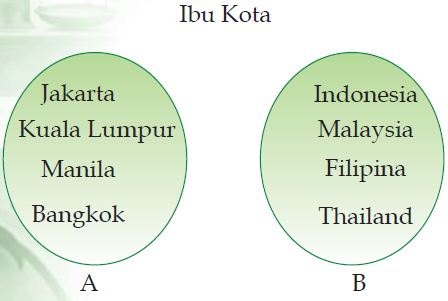 |
| Contoh: Pemetaan |
Pada relasi tersebut terlihat bahwa setiap anggota himpunan A mempunyai pasangan sempurna satu pada himpunan B.
Contoh korelasi lainnya perhatikan diagram panah nilai ulangan matematika 5 orang siswa kelas VIII berikut.
 |
| Contoh: Pemetaan |
Relasi tersebut mempunyai kekhususan menyerupai halnya korelasi antara himpunan A dan himpunan B, yaitu setiap anggota P mempunyai pasangan sempurna satu pada anggota himpunan Q.
Relasi antara himpunan A dan B serta korelasi antara himpunan P dan Q menyerupai ini dikenal dengan istilah pemetaan atau fungsi dari A ke B serta fungsi dari P ke Q.
Jadi, pemetaan atau fungsi dari himpunan A ke himpunan B yaitu korelasi khusus yang memasangkan setiap anggota himpunan A sempurna satu anggota pada himpunan B.
Pada fungsi kalian akan mengenal istilah domain atau tempat asal, kodomain atau tempat kawan, serta range atau tempat hasil.
Himpunan P = {Aam, Ilham, Trisno, Lisda, Dewi} disebut domain fungsi atau tempat asal. Himpunan Q = {6, 7, 8, 9, 10} disebut kodomain atau tempat kawan. Himpunan {7, 8, 9, 10} yang merupakan pasangan anggota tempat asal disebut tempat hasil atau range.
Perhattikan referensi berikut.
Suatu fungsi f dari himpunan A ke himpunan B dinyatakan dengan hukum x + 2, x ∈ A. Jika diketahui A = {2, 3, 5, 7} dan B = {1, 2, 3, …, 12}, tentukan:
a. Himpunan pasangan berurutan dalam f
b. Daerah asal, tempat kawan, dan tempat hasil dari f
Penyelesaian:
a. Pemetaan f dari A ke B yaitu f : x ® x + 2
x = 2 ⇒ f(x) = 2 + 2 = 4
x = 3 ⇒ f(x) = 3 + 2 = 5
x = 5 ⇒ f(x) = 5 + 2 = 7
x = 7 ⇒ f(x) = 7 + 2 = 9
Himpunan pasangan berurutan (x, f(x)) = {(2, 4), (3, 5), (5, 7), (7, 9)}
b. Daerah asal = {2, 3, 5, 7}
Daerah mitra = {1, 2, 3, …, 12}
Daerah hasil = {4, 5, 7, 9}
Fungsi dari himpunan A ke himpunan B dinotasikan dengan abjad kecil, contohnya f dan ditulis f: A ® B (dibaca f memetakananggota himpunan A ke anggota himpunan B).
Jika f yaitu sebuah fungsi dari himpunan A ke himpunanBdengan x ∈ A dan y ∈ B makapeta x oleh f yaitu y yang dinyatakan dengan f(x). Dengan demikian, diperoleh rumus fungsi sebagai berikut.
f : x ® y atau f : x ® g(x)
Istilah fungsi diperkenalkan oleh Gottfried Wilhelm Leibniz (1646 – 1716) hampir 50 tahun sehabis buku geometri dipublikasikan. Kemudian Leonard Euler (1707 – 1783) mengenalkan notasi fungsi sebagai y = f (x).
Penyajian Fungsi
Karena fungsi merupakan bentuk relasi, maka cara penyajian fungsi sama menyerupai cara penyajian korelasi sebelumnya. Suatu fungsi sanggup disajikan dalam bentuk diagram panah, diagram kartesius, dan himpunan pasangan terurut.
Baca selengkapnya: Rumus memilih banyaknya pemetaan
Sumber http://www.berpendidikan.com
0 Response to "Definisi Atau Pengertian Pemetaan (Fungsi) Dalam Matematika Beserta Cara Penyajiannya"
Posting Komentar