Pengertian Dan Pembuktian Dalil (Teorema) Pythagoras Beserta Penerapannya

Berikut ini ialah pembahasan wacana pythagoras yang mencakup pengertian dalil pythagoras, pembuktian dalil pythagoras, theorema phytagoras, teorema pythagoras, pembuktian teorema pythagoras, pembuktian teorema phytagoras, pembuktian rumus phytagoras.

Dalil Pythagoras

Seorang nakhoda kapal melihat puncak mercusuar yang berjarak 80 meter dari kapal. Jika diketahui tinggi mercusuar ialah 60 meter dari permukaan laut, dapatkah kalian memilih jarak nakhoda dari puncak mercusuar tersebut?

Persoalan di atas sanggup kita hitung dengan memakai prinsip segitiga siku-siku. Jika panjang dua sisi segitiga siku-siku kita ketahui, maka sisi yang lain sanggup kita tentukan. Caranya ialah dengan memakai dalil Pythagoras.

A. Pengertian Dalil Pythagoras

Dalam dalil Phytagoras melibatkan bilangan kuadrat dan akar kuadrat dalam sebuah segitiga.

Dalil Pythagoras ialah istilah lain dari teorema pythgoras yaitu bahwa sisi miring atau sisi terpanjang pada segitiga siku – siku sama dengan jumlah kuadrat sisi – sisi lainnya.

Oleh alasannya ialah itu, sebelum membahas lebih jauh dalil Pythagoras, marilah kita mengingat kembali bahan kuadrat bilangan, akar kuadrat bilangan, luas kawasan persegi, dan luas kawasan segitiga siku-siku.

1. Kuadrat dan Akar Kuadrat Bilangan

Masih ingatkah kalian bagaimana memilih kuadrat dari suatu bilangan?

Untuk memilih kuadrat dari suatu bilangan ialah dengan cara mengalikan bilangan tersebut dengan dirinya sendiri. 

Perhatikan teladan soal berikut ini!

Kebalikan dari kuadarat suatu bilangan ialah akar kuadrat. Misalkan, bilangan p yang tak negatif diperoleh p2 = 16. Maka bilangan p sanggup ditentukan dengan menarik √16 menjadi p = √16. Bilangan p yang diinginkan ialah 4 alasannya ialah 42 = 4 × 4 = 16. Bilangan p = 4 dinamakan akar kuadrat dari bilangan 16.

Jadi, akar kuadrat suatu bilangan ialah bilangan tak negatif yang apabila dikuadratkan akan menghasilkan bilangan yang sama dengan bilangan semula. 

Perhatikan teladan soal berikut!

2. Luas Daerah Persegi

Masih ingatkah kalian cara memilih luas berdiri datar persegi?

Luas persegi sanggup ditentukan dengan cara mengalikan sisi-sisinya. 

Jika sisi sebuah persegi ialah s maka luasnya sanggup dituliskan sebagai berikut.

L = s × s = s2

Perhatikan Contoh Soal Berikut!

3. Luas Daerah Segitiga

Kalian tentu sudah mempelajari cara menghitung luas dan keliling segitiga. Pada pembahasan ini kalian akan mempelajari hubungan antara luas segitiga dengan luas persegi panjang.

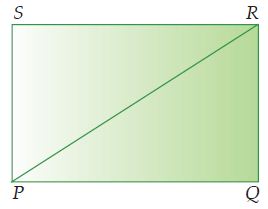
Perhatikan gambar persegi panjang PQRS berikut!

Dari persegi panjang tersebut kita memperoleh dua buah segitiga, yaitu ΔPQR dan ΔPSR. Luas ΔPQR = luas kawasan ΔPSR.

Hal ini mengatakan bahwa:

Luas ΔPQR = ½ × luas PQRS
                    = ½ × panjang PQ × panjang QR
                    = ½ × ganjal × tinggi

Jadi, luas segitiga dirumuskan:

L = ½ × a × t

Keterangan:
a = ganjal segitiga, dan
t = tinggi segitiga

Perhatikan teladan soal berikut!

B. Pembuktian Dalil Pythagoras

Luas persegi dan segitiga yang dibahas di atas sanggup dipakai untuk menenemukan dalil Pythagoras.

Untuk menemukan dalil Pythagoras lakukanlah acara berikut ini!

Berdasarkan acara di atas kalian akan memperoleh sifat segitiga siku-siku, yaitu pada setiap segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya. Sifat inilah yang kemudian dikenal dengan dalil Pythagoras.

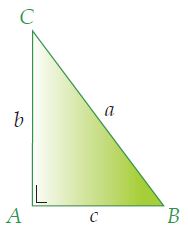
 Jadi, jikalau ABC ialah sembarang segitiga siku-siku dengan panjang sisi siku-siku a dan b serta panjang sisi miring c maka berlaku hubungan sebagai berikut:

c2 = a2 + b2

C. Penerapan Dalil Pythagoras

Dengan memakai dalil Pythagoras, kalian sanggup memilih panjang salah satu sisi segitiga siku-siku jikalau diketahui dua sisi yang lainnya.

Selain itu, dalil ini sanggup dipakai juga untuk memilih jenis segitiga dengan membandingkan kuadrat sisi miringnya dengan jumlah kuadrat sisi siku-sikunya.

Untuk lebih jelasnya, penerapan dalil Pythagoras sanggup dipakai untuk hal-hal berikut ini:

1. Menghitung panjang salah satu sisi segitiga siku-siku
2. Menentukan jenis segitiga jikalau diketahui panjang sisi-sisinya
3. Menghitung perbandingan sisi-sisi segitiga khusus
4. Menentukan panjang diagonal sisi dan diagonal ruang kubus

Penjelasan lebih lengkap untuk penerapan dalil pythagoras adalah;

1. Menghitung Panjang Salah Satu Sisi Segitiga Siku-Siku

Pada sebuah segitiga siku-siku, jikalau dua buah sisinya diketahui maka salah satu sisinya sanggup dicari dengan memakai dalil Pythagoras.

Perhatikan teladan soal berikut ini!

2. Menentukan Jenis Segitiga Jika Diketahui Panjang Sisi-Sisinya

Dalil Pythagoras sanggup dipakai untuk memilih jenis segitiga jikalau diketahui panjang sisi-sisinya. Namun demikian, sebelumnya akan dibahas terlebih dahulu mengenai kebalikan dari dalil Pythagoras.

a. Kebalikan Dalil Pythagoras

Pada bahasan sebelumnya telah dijelaskan bahwa kuadrat miring (hypothenusa) atau sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat panjang kedua sisinya.

Dari pernyataan tersebut kita peroleh kebalikan dari dalil Pythagoras, yaitu:

• Jika kuadrat sisi miring atau sisi terpanjang sebuah segitiga sama dengan jumlah kuadrat panjang kedua sisinya, maka segitiga tersebut merupakan segitiga siku-siku, atau
• Jika pada suatu segitiga berlaku a2 = b2 + c2, maka segitiga ABC tersebut merupakan segitiga siku-siku dengan besar salah satu sudutnya 90o.

Perhatikan teladan soal berikut!

b. Menentukan jenis segitiga jikalau diketahui panjang sisisisinya

Bagaimana memilih jenis segitiga jikalau diketahui panjang sisi-sisinya dengan memakai dalil Pythagoras? Coba kalian perhatikan teladan berikut ini.

Berdasarkan teladan di atas, dapatkah kalian memilih jenis segitiga jikalau diketahui panjang sisi-sisinya?

Berdasarkan teladan tersebut kalian akan menemukan hubungan panjang sisi-sisi sebuah segitiga dengan jenis segitiganya. Misalkan sisi terpanjang dari segitiga tersebut ialah c dan panjang sisi yang lainnya ialah a dan b, maka berlaku hubungan sebagai berikut.

1. Jika kuadrat sisi terpanjang sama dengan jumlah kuadrat sisisisi lainnya maka segitiga tersebut ialah segitiga siku-siku. (c2 = a2 + b2)
2. Jika kuadrat sisi terpanjang lebih besar dari jumlah kuadrat sisi-sisi lainnya maka segitiga tersebut ialah segitiga tumpul. (c2 > a2 + b2)
3. Jika kuadrat sisi terpanjang lebih kecil dari jumlah kuadrat sisi-sisi lainnya maka segitiga tersebut ialah segitiga lancip. (c2 < a2 + b2)

c. Tripel Pythagoras

Bilangan-bilangan 3, 4, dan 5 serta 6, 8, dan 10 merupakan bilangan-bilangan yang memenuhi dalil Pythagoras, yaitu 52 = 32 + 42 dan 102 = 62 + 82.

Bilangan-bilangan tersebut sanggup dipandang sebagai panjang sisi sebuah segitiga siku-siku. Bilangan-bilangan yang memenuhi dalil Pythagoras menyerupai itu disebut tripel Pythagoras.

Jadi, tripel Pythagoras adalah bilangan lingkaran positif yang kuadrat bilangan terbesarnya sama dengan jumlah kuadrat bilangan yang lainnya.

3. Menghitung Perbandingan Sisi-Sisi Segitiga Khusus

Segitiga siku-siku merupakan segitiga yang salah satu sudutnya membentuk sudut 90o. Bagaimana menghitung perbandingan sisi-sisi segitiga yang mempunyai ciri khusus menyerupai segitiga siku-siku, sama kaki, dan segitiga siku-siku yang salah satu sudutnya 30o? Perhatikan klarifikasi berikut ini!

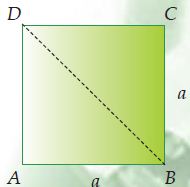
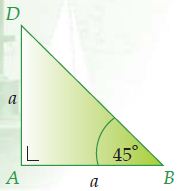
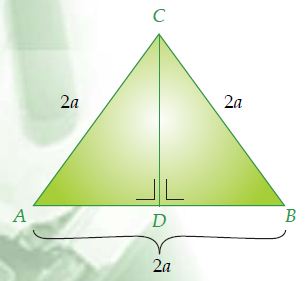
a. Segitiga siku-siku sama kaki

Segitiga siku-siku sama kaki diperoleh dengan cara membagi sebuah persegi melalui diagonalnya menjadi dua bagian. Perhatikan persegi ABCD yang panjang sisinya a menyerupai pada gambar di di bawah ini! 

Jika berdiri persegi tersebut dibagi dua melalui diagonal BD, maka akan diperoleh dua buah segitiga siku-siku sama kaki yaitu ΔBAD dan ΔBCD. Besar sudut ABD ialah 45o. Jelaskan mengapa?

Dengan memakai dalil Pythagoras kalian sanggup memilih panjang sisi BD yang belum diketahui. Berdasarkan dalil Pythagoras diperoleh hubungan sebagai berikut.

      BD2 = AB2 + AD2

⇔ BD2 = a2 + a2

⇔ BD2 = 2a2

⇔ BD  = √2a2 = a√2

Dengan demikian kita sanggup membandingkan panjang sisi-sisi segitiga siku-siku BAD sebagai berikut.

• AB : BD = a : a√2 = 1:√2
• AD : BD = a : a√2 = 1:√2
• AB : AD = a : a = 1 : 1
• AB : AD : BD = a : a : a√2 = 1 : 1 : √2

Perhatikan teladan soal berikut!

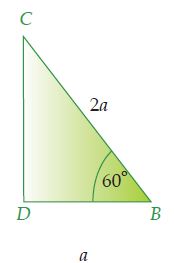
b. Segitiga siku-siku yang salah satu sudutnya 30o

Segitiga siku-siku yang salah satu sudutnya mem bentuk sudut 30o diperoleh dengan cara membagi sebuah segitiga sama sisi menjadi dua bagian. Perhatikan segitiga ABC di bawah ini!

Jika kita membagi dua segitiga sama sisi di atas menjadi dua bab yang sama besar maka akan diperoleh segitiga BDC siku-siku di D dan segitiga ADC siku-siku di D. Besar ∠DBC = 60o karena segitiga AB ialah segitiga sama sisi. Besar ∠BCD = 30o. Jelaskan mengapa?

Dengan memakai dalil Pythagoras kalian sanggup memilih panjang sisi CD yang belum diketahui. Berdasarkan dalil Pythagoras diperoleh hubungan sebagai berikut.

BC2 = BD2 + CD2

⇔ CD2 = BC2 – BD2

⇔ CD2 = (2a)2 – a2

⇔ CD2 = 4a2 – a2

⇔ CD2 = 3a2

⇔ CD = √3a2 = a√3

Dengan demikian kita sanggup membandingkan panjang sisi-sisi segitiga siku-siku BDC sebagai berikut.

• BD : BC = a : 2a = 1 : 2
• CD : BC = a √3 : 2a = √3 : 2
• BD : CD = a : a√3 = 1 : √3
• BD : CD : BC = a : a √3 : 2a = 1 : √3 : 2

Perhatikan Contoh Soal Berikut!

4. Menentukan Panjang Diagonal Sisi dan Diagonal Ruang Kubus

Dalil Pythagoras sanggup dipakai untuk mencari panjang diagonal sisi atau diagonal ruang kubus dan balok. Hal ini dikarenakan diagonal sisi dan diagonal ruang merupakan sisi miring bagi sisi bidangnya.

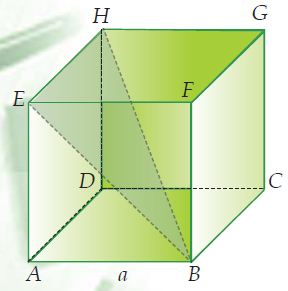
Perhatikan gambar kubus ABCD.EFGH di bawah ini!

Pada kubus ABCD.EFGH rusuk EB merupakan salah satu diagonal sisi pada kubus dan rusuk HB merupakan salah satu diagonal ruangnya. Jika panjang sisi kubus ABCD.EFGH ialah a satuan panjang maka kita sanggup memilih panjang rusuk EB dan HB.

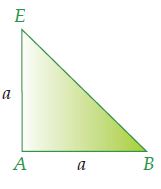
Untuk memilih panjang diagonal sisi EB, perhatikan segitiga siku-siku ABE pada kubus ABCD. EFGH. Berdasarkan dalil Pythagoras diperoleh hubungan sebagai berikut.

EB2 = AB2 + AE2
⇔ EB2 = a2 + a2
⇔ EB2 = 2a2
⇔ EB = √2a2 = a√2

Jadi, panjang diagonal sisi sebuah kubus yang panjang sisinya a ialah a√2 .

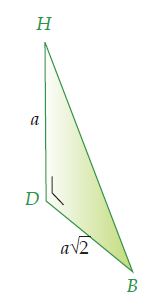
Untuk memilih panjang diagonal ruang HB, perhatikan segitiga BDH yang siku-siku di D. Karena rusuk BD merupakan di agonal sisi kubus ABCD.EFGH, maka panjangnya ialah a√2.

Dengan memakai dalil Pythagoras diperoleh hubungan berikut.

      HB2 = DB2 + DH2
⇔ HB2 = (a√2 )2 + a2
⇔ HB2 = 2a2 + a2
⇔ HB2 = 3a2
⇔ HB = √3a2 = a√3

Jadi, panjang diagonal ruang sebuah kubus yang panjang sisinya a satuan ialah a√3 .

Perhatikan teladan soal berikut!

Baca juga: 150 Daftar Bilangan Tripel Pythagoras

Sumber http://www.berpendidikan.com

Share this post

Berlangganan update artikel terbaru via email: