Rumus Integral Substitusi Referensi Soal Beserta Pembahasannya

Rumusbilangan.com- Pada pembahasan kali ini, kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola soal intergral substitusi dan pembahasannya lengkap.

Dalam soal integral memiliki banyak keragaman tersendiri, sehingga dalam penyelesaiannya juga memerlukan metode – metode yang bermacam-macam tersendiri pula. Untuk itu, kita harus sanggup memahami suatu metode – metode yang sempurna untuk menuntaskan banyak sekali ragam soal integral.

Untuk itu, melalui artikel ini, kita akan membahas bahan mengenai rumus – rumus dan pola – pola dari soal integral tersebut. Oleh lantaran itu marilah kita simak pembahasannya …

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya — Integral Subtitusi

Pengertian Integral Subtitusi

Di dalam bidang kalkulasi, integral substitusi atau substitusi – u ialah salah satu metode untuk mencari suatu integral dengan mensubstitusi salah satu variabel dan mengubahnya menjadi sebuah bentuk yang lebih sederhana.

Contohnya:

Contoh 1:

Perhatikan sebuah integral berikut:

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Apabila kita melaksanakan substitusi u = (x² + 1), maka diperolehlah du = 2x dx, maka sehingga x dx = ½du. Lalu kita substitusikan ke dalam sebuah bentuk integralnya:

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Perlu diingat bahwa di pembahasan ini batas bawahnya yaitu: x = 0, diganti dengan u = 0² + 1 = 1, dan batas atas x = 2 diganti dengan u = 2² + 1 = 5, maka dalam perkara ini u tidak perlu diubah kembali menjadi x.

Contoh 2:

Untuk sebuah integral:

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Substitusi yang sebaiknya dilakukan yaitu: x = sin(u), dx = cos(u) du, sebab $kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya$ :

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Contoh 3:

Metode substitusi ini sanggup dipakai untuk mencari antiturunan, yaitu dengan memilih korelasi antara x dan u serta dx dan du. Berikut ini ialah contohnya:

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Rumus integral substitusi dipakai pada serpihan dari sebuah fungsi merupakan suatu turunan dari fungsi lainnya. Biasanya, soal integral yang sanggup diselesaikan dengan cara memakai substitusi yang terdiri dari 2 faktor , yang mana turunan dari salah satu faktornya memiliki sebuah korelasi dengan faktor lainnya.

Rumus Integral Subtitusi

Pada serpihan awal kita sudah sedikit membahas ihwal ciri – ciri soal integral yang sanggup diselesaikan dengan memakai sebuah rumus integral substitusi.

yang mana intinya, ciri – ciri dari soal integral yang sanggup diselesaikan dengan memakai rumus integral substitusi yaitu yang memiliki faktor yang merupakan turunan dari faktor lainnya.

Coba kita perhatikan salah satu pola soal integral yang sanggup diselesaikan dengan memakai rumus integral substitusi di bawah berikut:

Soal integral yang diberikan di atas berikut yakni sebuah soal yang tidak sanggup diselesaikan dengan memakai rumus integral umum menyerupai biasa.

Perlu sebuah teknik dan metode yang sempurna untuk mendapat nilai integralnya. Metode yang sempurna untuk menuntaskan soal integral di atas yaitu rumus integral substitusi.

Rumus integral substitusi sanggup diberikan dengan melalui persamaan di bawah berikut ini:

Contoh Soal Integral Subsitusi

Selanjutnya kita coba bahas pola soalnya berikut ini:

Coba kita perhatikan kembali soal integral yang diberikan berikut ini:

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Turunan dari $kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya$ ialah $kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya$ .

Maka, dengan demikian, kita sanggup menerka bahwa soal integral di atas sanggup diselesaikan dengan memakai sebuah rumus integral substitusi, dengan pemisalan sebagai berikut: $kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya$ .

Perhatikanlah proses lengkapnya yang akan di bawah ini:

Contoh:

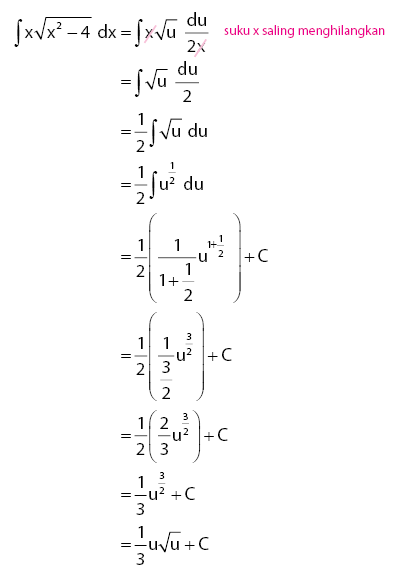
kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Maka,

kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Sesudah kita mendapat hasil simpulan dalam persamaan u, maka kita perlu mengembalikan kembali pemisalan $kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya$ yang kita lakukan di awal.

Maka, karenanya ialah menyerupai berikut:

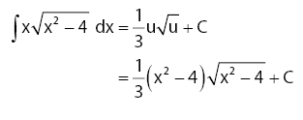
kita akan membahas makalah mengenai bahan tentang rumus integral substitusi dan pola s Rumus Integral Substitusi Contoh Soal Beserta Pembahasannya

Untuk lebih mantapnya, mari kita coba membahas soal lagi berikut:

Contoh 1:

Tentukanlah dari ∫ x² (x³ + 5)⁷ dx = …

Pembahasan :
Misalkan : u yakni x³ + 5
$\frac{d u}{d x}$ = 3x² ⇔ $\frac{d u}{3}$ = x² dx
$\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$ $\begin{aligned} \int x^{2} (x^{3} + 5)^{7} d x & = \int (x^{3} + 5)^{7} x^{2} d x \\ = \int u^{7} \frac{d u}{3} \\ = \frac{1}{3} \int u^{7} d u \\ = \frac{1}{3} \cdot \frac{1}{8} u^{8} + C \\ = \frac{1}{24} u^{8} + C \\ = \frac{1}{24} (x^{3} + 5)^{8} + C \end{aligned}$

Contoh 2:

$\int \frac{4 x}{\sqrt{x^{2} - 2}}$ dx = …

Pembahasan:
Misalkan : u = x² – 2
$\frac{d u}{d x}$ = 2x ⇔ $\frac{d u}{2}$ = x dx
$\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$ $\begin{aligned} \int \frac{4 x}{\sqrt{x^{2} - 2}} d x & = 4 \int \frac{1}{\sqrt{x^{2} - 2}} \cdot x d x \\ = 4 \int \frac{1}{\sqrt{u}} \cdot \frac{d u}{2} \\ = \frac{4}{2} \int u^{- \frac{1}{2}} d u \\ = 2 \cdot 2 u^{\frac{1}{2}} + C \\ = 4 \sqrt{u} + C \\ = 4 \sqrt{x^{2} - 2} + C \end{aligned}$

Demikianlah pembahasan kita hari ini mengenai Rumus Integral Subtitusi. Semoga bermanfaat ….

Baca Juga:

Sumber aciknadzirah.blogspot.com

iklan banner

Rumus Integral Substitusi Referensi Soal Beserta Pembahasannya

Pengertian Integral Subtitusi

Contohnya:

Contoh 1:

Contoh 2:

Contoh 3:

Rumus Integral Subtitusi

Contoh Soal Integral Subsitusi

Contoh 1:

Contoh 2:

0 Response to "Rumus Integral Substitusi Referensi Soal Beserta Pembahasannya"

Posting Komentar

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel