Cara Memilih Titik Potong Dua Buah Garis Yang Tidak Sejajar
Berikut ini yakni pembahasan wacana bagaimana cara memilih titik potong dari dua buah garis yang tidak sejajar.
Titik Potong Dua Buah Garis
Dua buah garis yang tidak sejajar akan berpotongan di satu titik.
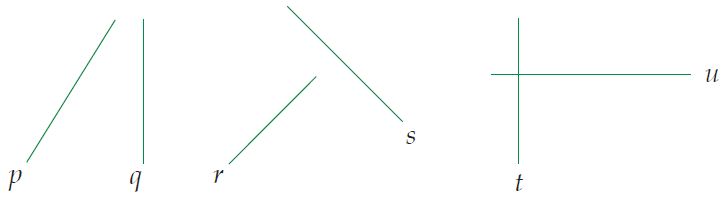
Perhatikan gambar di bawah ini!
Pada gambar terlihat bahwa garis p dan q , garis r dan s, serta garis t dan u akan berpotongan di satu titik. Misal terdapat dua buah garis yang tak sejajar dengan persamaan y = a1x + b1 dan y = a2x + b2, a1 ≠ a2 dan berpotongan di titik (x0, y0).
Titik perpotongan dua garis tersebut sanggup dicari dengan mensubstitusikan (x0, y0) ke masing-masing persamaan, sehingga diperoleh:
y0 = a1 x0 + b1 … (1)
y0 = a2 x0 + b2 … (2)
Dari persamaan (1) dan (2) diperoleh:
- a1 x0 + b1 = a2 x0 + b2
- a1x0 – a2 x0 = b2 – b1
- x0(a1 – a2) = b2 – b1
- x0 = (b2 – b1):(a1 – a2)
Untuk mencari nilai y0 sanggup dilakukan dengan cara mensubstitusikan nilai x0 ke dalam persamaan (1) atau persamaan (2). Misalkan kita memasukkan nilai x0 ke persamaan (1) sehingga diperoleh:
Contoh Soal dan Pembahasannya
Tentukan titik potong garis y = 2x – 4 dan y = -3x + 6!
Penyelesaian:
Cara I
a1 = 2; b1 = –4; a2 = –3; b2 = 6
Kaprikornus titik potongnya yakni (2, 0)
Cara II
y = 2x – 4 … (1)
y = –3x + 6 … (2)
Dari (1) dan (2) diperoleh:
2x – 4 = –3x + 6
2x + 3x = 6 + 4
5x = 10
x = 2
Substitusi x = 2 ke persamaan (1) atau (2) sehingga:
y = –3x + 6
y = –3(2) + 6 = –6 + 6 = 0
Jadi titik potongnya yakni (2, 0)
Baca Juga: Rumus Mencari Gradien Garis
Sumber http://www.berpendidikan.com
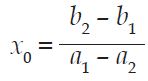
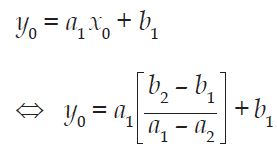
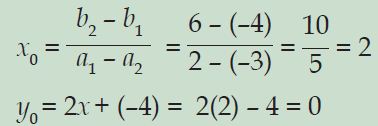
0 Response to "Cara Memilih Titik Potong Dua Buah Garis Yang Tidak Sejajar"
Posting Komentar