Pengertian Dan Rumus Persamaan Garis Lurus Serta Pola Soal Persamaan Garis Lurus Dan Pembahasannya
Berikut ini yakni pembahasan lengkap ihwal Persamaan Garis Lurus yang mencakup Pengertian Persamaan Garis, Pengertian Persamaan Garis lurus, Menggambar Garis Lurus Pada Bidang Kartesius, persamaan garis lurus, rumus persamaan garis, contoh soal persamaan garis lurus, rumus persamaan garis lurus, rumus persamaan garis tegak lurus.
Dalam melaksanakan sebuah pendakian, para pendaki niscaya akan melewati banyak sekali jenis jalanan. Adakalanya mereka menemui jalan yang lurus, terjal dan berkelok-kelok. Tidak jarang mereka pun menghadapi jalan yang curam dan menanjak dengan kemiringan tertentu.
Persamaan Garis Lurus
Pada ketika duduk di dingklik sekolah dasar, kalian pernah mempelajari sistem koordinat kartesius, bukan? Coba kalian ingat-ingat kembali. Persamaan garis yang akan kita bahas kali ini juga disajikan dalam sistem koordinat kartesius.
1. Sistem Koordinat Kartesius
Untuk memilih letak suatu benda yang berada di ruangan tertentu kita memakai sebuah koordinat. Pada koordinat kartesius terdapat dua buah garis yang menjadi contoh dalam memilih posisi atau letak suatu titik. Kedua garis ini saling tegak lurus dan berpotongan di titik sentra (0,0).
Garis-garis yang saling tegak lurus ini untuk selanjutnya disebut sebagai sumbu koordinat. Letak sebuah titik pada sistem koordinat kartesius ditentukan oleh pasangan absis x dan ordinat y.
Contoh Soal dan Pembahasannya
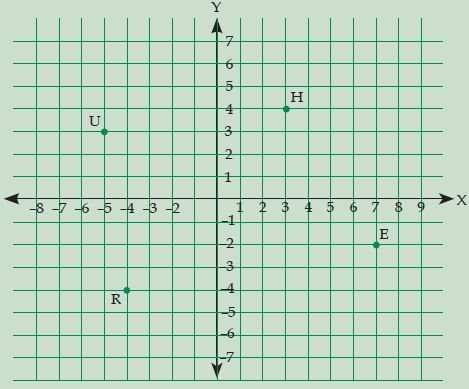
Tentukanlah letak titik H, E, R, dan U pada sistem koordinat berikut!
Penyelesaian:
H = (3, 4) ; E = (7, -2) ; R = (-4, -4) ; U = (-5, 3)
2. Pengertian Persamaan Garis
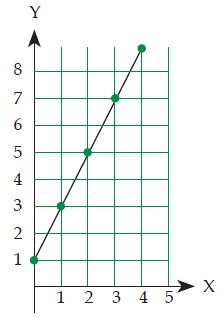
Jika diketahui sebuah pemetaan f(x) = 2x + 1 dengan tempat asal 0 < x < 5 dengan x Î R, maka kalian sanggup menggambarkan grafik fungsinya ibarat gambar di bawah ini.
Dalam permasalahan tersebut, persamaan f(x) = 2x + 1 sanggup kita ubah menjadi persamaan y = 2x + 1.
Dalam grafik terlihat bahwa grafik fungsinya berupa garis lurus, mengapa demikian? Persamaan y = 2x + 1 disebut persamaan garis lurus atau persamaan garis. Secara umum bentuk persamaan garis yakni sebagai berikut.
px + qy = r dimana p ≠ 0 dan q ≠ 0
Jika masing masing ruas dari persamaan px + qy = r kita bagi dengan q maka akan diperoleh persamaan garis berikut.
y = -(p/q)x + r/q
Bilangan di depan variabel x, yaitu –p/q merupakan sebuah konstanta sehingga sanggup kita ubah menjadi konstanta lain contohnya m, dan r/q sanggup kita ganti dengan c. Untuk selanjutnya kita peroleh persamaan garis yang gres sebagai berikut.
y = mx + c, dengan m dan c yakni sebuah konstanta.
Contoh Soal dan Pembahasannya
Nyatakan persamaan garis berikut ke dalam bentuk y = mx + c!
a. 3x + 4y = 12
b. 4x – 2y – 6 = 0
Penyelesaian:
a. 3x + 4y = 12
==> 4y = –3x + 12
==> y = –¾x + 3
b. 4x – 2y – 6 = 0
==> –2y = –4x + 6
==> y = 2x – 3
3. Menggambar Garis Lurus Pada Bidang Kartesius
Untuk menggambar sebuah garis kalian cukup memilih dua buah titik yang memenuhi persamaan garis yang diberikan. Untuk menggambar garis dengan persamaan y = mx + c, langkah-langkahnya yakni sebagai berikut.
- Tentukan dua buah titik yang memenuhi persamaan y = mx + c dengan cara memasukkan nilai x pada persamaannya
- Tarik garis lurus pada kedua titik tersebut
Perhatikan contoh berikut.
Contoh Soal dan Pembahasannya
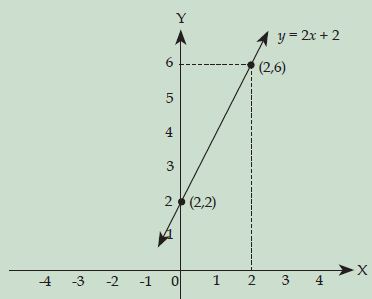
Gambarkan grafik persamaan garis y = 2x + 2!
Penyelesaian:
Persamaan garis y = 2x + 2 akan melewati titik (0, 2) dan (2, 6).
Dari contoh di atas sanggup dibuktikan bahwa hanya dengan dua buah titik kita sanggup menggambar sebuah garis.
4. Menentukan Persamaan Garis yang Digambar Pada Bidang Kartesius
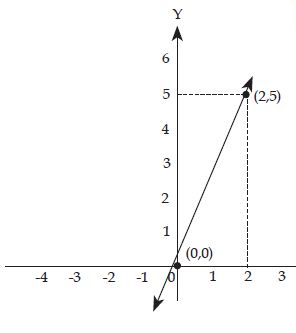
Tahukah kalian bagaimana memilih persamaan garis apabila diketahui gambarnya pada bidang kartesius? Perhatikan gambar persaman garis di bawah ini!
Misalkan persamaan garis pada gambar di samping yakni y = mx + c. Kita sanggup memilih nilai m dan c alasannya terdapat dua buah titik yang dilewati oleh persamaan garis tersebut, yaitu titik (0,0) dan (2, 5).
Kedua titik tersebut kemudian disubstitusikan ke dalam persamaan y = mx + c sehingga diperoleh hasil sebagai berikut.
(0, 0) 0 = m(0) + c
c = 0
(2, 5) 5 = m(2) + c
5 = 2m + 0
m = 5/2
Jadi, persamaan garis pada gambar tersebut yakni y = (5/2)x.
Dari permasalahan tersebut sanggup ditarik kesimpulan bahwa persamaan garis yang melalui titik sentra (0,0) dan titik (a, b) dengan a ≠ 0 yakni y = (b/a)x.
Contoh Soal dan Pembahasannya
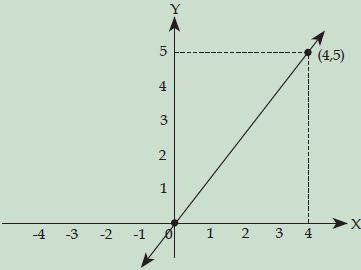
Tentukan persamaan garis dari gambar di bawah ini!
Penyelesaian:
a = 4, dan b = 5. Persamaan garisnya yakni y = (5/4)x
Dalam kasus khusus, persamaan garis lurus yang sejajar dengan sumbu X mempunyai bentuk y = c. Sedangkan persamaan garis yang sejajar sumbu Y mempunyai bentuk x = c, dimana c yakni konstanta.
Baca juga: Cara Menentukan Persamaan Garis Lurus


0 Response to "Pengertian Dan Rumus Persamaan Garis Lurus Serta Pola Soal Persamaan Garis Lurus Dan Pembahasannya"
Posting Komentar