Persamaan Garis Singgung Bulat Dan Rujukan Soal Garis Singgung Lingkaran
Berikut ini ialah pembahasan wacana persamaan garis singgung lingkaran, teladan soal garis singgung lingkaran, garis singgung bundar smp kelas 8, teladan soal persamaan garis singgung lingkaran, soal garis singgung bundar smp kelas 8.
Persamaan Garis Singgung Lingkaran
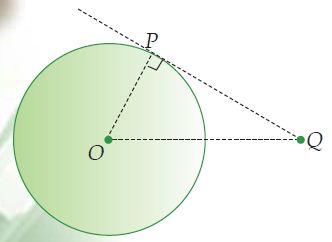
Untuk mengetahui panjang garis singgung lingkaran, perhatikan gambar di bawah ini! PQ ialah garis singgung bundar yang tegak lurus dengan OP, dimana OP merupakan jari-jari lingkaran, dan OQ jarak antara titik sentra bundar dengan titik yang berada di luar lingkaran.
Jika kau perhatikan dengan jelas, ΔOPQ ialah segitiga siku-siku dengan siku-siku di P.
Berdasarkan teorema Phythagoras sanggup dinyatakan sebagai berikut.
OQ2 = OP2 + PQ2
PQ2 = OQ2 – OP2
Jadi, sanggup disimpulkan bahwa panjang garis singgung bundar adalah:
g2 = p2 – r2
Keterangan:
g : Panjang garis singgung
p : Jarak antara titik sentra bundar dengan titik yang berada di luar lingkaran
r : Jari-jari lingkaran
Contoh Soal Garis Singgung Lingkaran
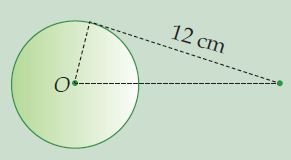
Panjang garis singgung yang melalui titik di luar bundar ialah 12 cm. Panjang jari-jari lingkarannya 5 cm. Hitunglah jarak antara titik tersebut dengan sentra lingkarannya!
Penyelesaian:
Jari-jari bundar (r) = 5 cm
Panjang garis singgung (g) = 12 cm
Maka, g2 = p2 – r2
122 = p2 – 52
144 = p2 – 25
p2 = 144 + 25
= 169
p = √169
=13 cm
Jadi, jarak antara titik dengan sentra bundar ialah 13 cm.
Baca juga: Melukis Garis Singgung Lingkaran
Sumber http://www.berpendidikan.com
0 Response to "Persamaan Garis Singgung Bulat Dan Rujukan Soal Garis Singgung Lingkaran"
Posting Komentar