Operasi Hitung Bilangan Bundar Faktual Dan Negatif Lengkap
Setelah mengetahui pengertian bilangan bundar beserta contohnya, pada pembahasan kali ini akan dijelaskan perihal operasi hitung pada bilangan bundar yang mencakup penjumlahan bilangan bulat, pengurangan bilangan bulat, perkalian bilangan bulat, dan pembagian bilangan bulat.
Operasi Bilangan Bulat
1. Operasi penjumlahan bilangan bulat
Penjumlahan pada bilangan bundar sanggup diselesaikan dengan memakai garis bilangan. Pada garis bilangan telah disepakati bahwa arah bilangan bundar nyata ke kanan dan arah bilangan bundar negatif ke kiri.
Agar lebih terperinci perhatikan ketentuan berikut ini:
- Bilangan nyata + bilangan nyata = bilangan positif.
- Bilangan negatif + bilangan negatif = bilangan negatif.
- Bilangan nyata + bilangan negatif = bilangan nyata atau negatif.
- Jika bilangan nyata > bilangan negatif karenanya bilangan positif.
- Jika bilangan nyata < bilangan negatif karenanya bilangan negatif.
Untuk Lebih Jelasnya perhatikan pola berikut:
Hitunglah penjumlahan:
a. 4 dan 5
b. 5 dan (–2).
Penyelesaian:
a. Dari nol sebagai titik pangkal, kita melangkah 4 satuan ke kanan, dilanjutkan dengan 5 satuan ke kanan. Hasil penjumlahannya yaitu jarak dari titik nol ke posisi terakhir, yaitu 9.
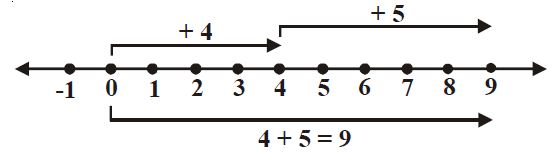 |
| Jadi 4 + 5 = 9 |
b. Dari titik nol kita melangkah 5 satuan ke kanan, kemudian melangkah 2 satuan ke kiri. Hasil penjumlahannya yaitu 3.
Jadi, 5 + (–2) = 3
Baca selengkapnya: Sifat-sifat penjumlahan pada bilangan bulat
2. Operasi pengurangan bilangan bulat
Pengurangan sebagai penjumlahan dengan lawan pengurangannya, misalnya:
1. 8 – 5 = 8 + (–5) = 3
Jadi, 8 – 5 = 8 + (–5)
2. –1 – 4 = –1 + (–4) = –5
3. 9 – (–5) = 9 + 5 = 14
Untuk lebih jelasnya perhatikan kaidah pengurangan pada bilangan bundar berikut ini!
Untuk setiap a dan b bilangan bundar berlaku:
- a – b = a + (–b)
- a –(–b) = a + b
- –a – (–b) = –a + b
- –a – b = –a + (–b)
3. Operasi perkalian bilangan bulat
Di Sekolah Dasar, kalian telah mempelajari perkalian yang juga berarti penjumlahan berulang.
Misalkan 5 x 4 = 4 + 4 + 4 + 4 + 4 atau a x b = b + b + b + … + b (sebanyak a kali)
a. Perkalian Bilangan Bulat Positif dan Negatif
Perhatikanlah contoh-contoh berikut ini:
1. 1 x (–5) = –5
2. 2 x (–5) = –10
3. 3 x (–5) = –15
4. 4 x (–5) = –20
5. 5 x (–5) = –25
Berdasarkan contoh-contoh di atas sanggup disimpulkan bahwa hasil kali bilangan bundar nyata dengan bilangan bundar negatif yaitu bilangan bundar negatif.
Untuk setiap bilangan bundar a dan b selalu berlaku a x (– b) = – (a x b).
b. Perkalian Dua Bilangan Bulat Negatif
Perhatikanlah contoh-contoh berikut ini:
1. 3 x (–3) = –9
2. 2 x (–3) = –6
3. 1 x (–3) = –3
4. 0 x (–3) = 0
5. –1 x (–3) = 3
6. –2 x (–3) = 6
7. –3 x (–3) = 9
Dari pola 5, 6, dan 7 di atas hasil kali dua bilangan bundar negatif yaitu bilangan bundar positif.
Untuk setiap bilangan bundar a dan b selalu berlaku (– a) x (– b) = (a x b).
c. Perkalian Bilangan Bulat dengan Nol (0)
Perhatikan perkalian berikut ini!
1. 5 x 0 = 0
2. –3 x 0 = 0
3. 0 x 2 = 0
Untuk semua bilangan apabila dikalikan dengan nol (0) karenanya yaitu nol.
Untuk setiap bilangan bundar a selalu berlaku a x 0 = 0 x a = 0.
d. Unsur Identitas pada Perkalian
Semua bilangan bundar bila dikalikan dengan 1 atau sebaliknya, akan menghasilkan bilangan itu sendiri. Dalam hal ini 1 disebut unsur identitas pada perkalian.
Misalnya:
1. 10 x 1 = 10
2. 5 x 1 = 5
3. –5 x 1 = –5
4. –3 x 1 = –3
Untuk setiap bilangan bundar a selalu berlaku a x 1 = 1 x a = a.
Baca selengkapnya: Sifat-sifat perkalian pada bilangan bulat
4. Operasi pembagian bilangan bulat
Misalkan ditentukan p x 8 = 48. Untuk mencari nilai p sanggup dilakukan dengan dua cara yaitu:
a. Cara perkalian, yaitu dengan mencari suatu bilangan yang kalau dikalikan dengan 8 karenanya 48 di mana bilangan itu yaitu 6.
b. Cara pembagian, yaitu dengan membagi 48 dengan 8, yang karenanya yaitu 6.
Dengan demikian, membagi 48 dengan 8 sama artinya dengan mencari suatu bilangan yang kalau dikalikan dengan 8 karenanya sama dengan 48 yang berarti 48 : 8 = 6 <=> 6 x 8 = 48.
Berdasarkan uraian di atas sanggup disimpulkan bahwa: pembagian merupakan operasi kebalikan dari perkalian, secara umum sanggup dituliskan:
a : b = c <=> b x c = a ; b ¹ 0
Bentuk a : b sanggup juga ditulis: a/b
Contoh
1. 30 : 5 = 6 alasannya yaitu 5 x 6 = 30
2. 16 : (–4) = –4 alasannya yaitu –4 x (–4) = 16
3. –10 : 5 = –2 alasannya yaitu 5 x (–2) = –10
4. –8 : (–2) = 4 alasannya yaitu –2 x 4 = –8
Dari contoh-contoh di atas sanggup disimpulkan bahwa:
- hasil bagi dua bilangan bundar nyata yaitu bilangan positif,
- hasil bagi dua bilangan bundar negatif yaitu bilangan bundar positif,
- hasil bagi bilangan bundar nyata dengan bilangan bundar negatif atau sebaliknya yaitu biangan negatif.
a. Pembagian Bilangan Bulat dengan Nol (0).
Misalkan 5 : 0 = p <=> 0 x p = 5
Tidak ada satu pun pengganti p pada bilangan bundar yang memenuhi 0 x p = 5, sehingga sanggup disimpulkan bahwa:
Untuk setiap bilangan bundar a, a : 0 tidak terdefinisi
b. Pembagian Bilangan Bulat oleh Nol (0).
Untuk pembagian 0 : 3 = n, adakah pengganti n yang memenuhi?
Perhatikan uraian berikut:
0 : 3 = n <=> 3 x n = 0
Pengganti n yang memenuhi 3 x n = 0, yaitu 0.
Jadi, kesimpulannya adalah
Untuk setiap bilangan bundar a, berlaku 0 : a = 0
Baca selengkapnya; Perpangkatan pada Bilangan bulat
Demikian pembahasan perihal operasi hitung pada bilangan bundar yang disajikan secara lengkap.
Baca juga: Sifat perkalian bilangan Bulat
Sumber http://www.berpendidikan.com
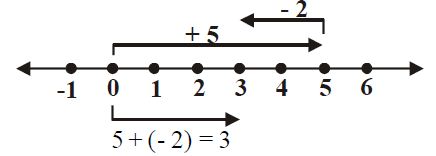
0 Response to "Operasi Hitung Bilangan Bundar Faktual Dan Negatif Lengkap"
Posting Komentar