Penjelasan Rumus Phytagoras Dan Pola Soal Serta Pembahasannya

Penjelasan Rumus Phytagoras Dan Contoh Soal Serta Pembahasannya – Kali ini kita akan membahas bahan perihal rumus phytagoras disertai contoh-contoh soalnya.

Perhatikan gambar dibawah berikut:

Ilustrasi Gambar Tangga

Jika diperhatikan, bisakah kita mentukan berapa ukuran panjang tangga tersebut tanpa harus menaikinya? Salah satu cara untuk memilih panjang tangga ialah dengan memakai rumus phytagoras. Kemudian apa itu rumus phytagoras?Bagaimana penerapannya dalam kehidupan?

Untuk menjawab pertanyaan-pertanyaan tersebut, mari kita simak pembahasannya dibawah berikut ini:

Pengertian Rumus Phytagoras

Rumus Phytagoras ialah sebuah rumus yang didapat dari teorema Phytagoras. Teorema Phytagoras yaitu sebuah teorema yang menunjukan perihal keberhubungan sisi-sisi yang terdapat dalam sebuah segitiga siku-siku.

Teori ini pertama kali dikemukakan oleh seorang matematikawan yang berasal dari Yunanni yang berjulukan Phytagoras.

Bunyi dari teorema phytagoras yaitu sebagai berikut:

Pada sebuah segitiga siku-siku, kuadrat dari sisi terpanjang yaitu sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.

Berdasarkan teorema tersebut sanggup dibentuk sebuah rumus yang sanggup digambarkan sebagai berikut:

Gambar Segitiga Siku-Siku

Dari gambar segitiga siku-siku diatas, pada abjad B. Apabila panjang sisi miring (hipotenusa) ialah c dan panjang sisi-sisi penyikunya (sisi selain sisi miring) ialah a dan b, maka teorema Phytagoras di atas sanggup dirumuskan sebagai berikut:

Rumus Phytagoras

c² = a²  + b²

Keterangan:
c = sisi miring
a = tinggi
b = alas

Pada umumnya, rumus phytagoras dipakai untuk mengetahui ukuran sebuah panjang sisi miring segitiga siku-siku, yaitu :

Berdasarkan gambar segitiga siku-siku diatas, maka sanggup dirumuskan yaitu:

Kuadrat sisi AC = kuadrat sisi AB + kuadrat sisi BC. atau AC² = AB² + BC²

Rumus untuk mencari panjang sebuah sisi alas:
b² = c²  – a²
Rumus untuk mencari sebuah sisi samping/tinggi segitiga:
a² = c²  – b²
Rumus untuk mencari sebuah sisi miring segitiga siku-siku:
c² = a²  + b²

Setelah kita mempelajari beberapa pemaparan perihal rumus phytagoras diatas, tibalah saatnya kita kini bagamana menerapkan rumus tersebut.

Contoh Soal Dan Pembahasannya

Secara matematis, rumus phytagoras ini biasa dipakai untuk memilih panjang sisi dari sebuah segitiga siku-siku. Maka dari itu untuk lebih jelasnya, mari kita perhatikan contoh-contoh soal di bawah berikut ini:

Contoh Soal 1 :

Diketahui sebuah segitiga siku-siku ABC dengan siku-siku di B digambarkan sebagai berikut:

Tentukanlah panjang sisi miring AC pada gambar di atas:

Jawab:
Karena segitiga di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras sebagai berikut:
AC² = AB² + BC²
AC² = 10² + 8²
AC² = 100 + 64
AC² = 164
AC  =  √164
AC  = 12.8
Maka, panjang sisi AC pada segitiga siku-siku tersebut yaitu 12.8 cm.

Contoh Soal 1 :

Diketahui sebuah segitiga siku-siku ABC dengan siku-siku di B digambarkan sebagai berikut:

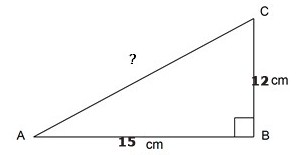
Tentukanlah panjang sisi miring AC pada gambar di atas:

Jawab:
Karena segitiga di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras sebagai berikut:
AC² = AB² + BC²
AC² = 15² + 12²
AC² = 225 + 144
AC² = 369
AC  =  √369
AC  = 19.2
Maka, panjang sisi AC pada segitiga siku-siku tersebut yaitu 19.2 cm.

Demikianlah pembahasan mengenai rumus phytagoras. Semoga bermanfaat … Aamiin

Baca Juga:

• Bilangan Berpangkat Pecahan – Pengertian, Sifat, Rumus, Contoh Soal
• Cara Menghitung 1 Tahun berapa Hari? Serta Contoh Soalnya

Sumber aciknadzirah.blogspot.com

Share this post

Berlangganan update artikel terbaru via email: