Cara Memilih Persamaan Garis Lurus Lengkap Dengan Pola Soal Dan Pembahasannya
Berikut ini yaitu pembahasan perihal bagaimana cara Menentukan Persamaan Garis lurus dengan banyak sekali keadaan dan kondisi diantaranya persamaan garis melalui 2 titik, tumpuan soal persamaan garis tegak lurus, tumpuan soal hubungan dua garis lurus.
Cara Menentukan Persamaan Garis Lurus
Jika diketahui gradien sebuah garis yang melalui suatu titik tertentu, dapatkah kalian memilih persamaan garisnya? Atau dapatkah kalian memilih gradien sebuah garis jikalau yang diketahui hanya dua buah titik yang dilalui oleh garis tersebut?
1. Menentukan Persamaan Garis yang Melalui Sebuah Titik (a,b) dengan Gradien m
Kalian semua niscaya sudah mengenal bentuk umum dari persamaan garis, yaitu y = mx + c. Untuk memilih persamaan garis yang melalui titik (a, b) dengan gradien m, substitusikan x = a dan y = b pada persamaan garis y = mx + c sehingga diperoleh:
b = ma + c atau c = b – ma
Langkah selanjutnya yaitu mensubstitusikan nilai c pada persamaan awal, yaitu y = mx + c sehingga diperoleh:
y = mx + (b – ma)
y – b = mx – ma
y – b = m(x – a)
Jadi, persamaan garis yang melalui titk (a, b) dengan gradien m yaitu y – b = m(x – a).
Contoh Soal dan Pembahasannya
Tentukan persamaan garis yang melalui titik (-4, 5) dengan gradien 2!
Penyelesaian:
a = –4;
b = 5;
m = 2
y – b = m(x – a) ⇔ y – 5 = 2(x – (–4))
⇔ y – 5 = 2(x + 4)
⇔ y – 5 = 2x + 8
⇔ y = 2x + 13
2. Menentukan Persamaan Garis yang Melalui Titik (x1, y1) dan (x2, y2)
Kalian masih ingat cara mencari gradien garis yang melalui dua buah titik. Coba kalian ingat-ingat kembali bagaimana cara mencari gradien apabila diketahui dua buah titik, misalkan (x1, y1) dan (x2, y2)!
Gradien garis yang melalui titik tersebut adalah
Dengan memakai rumus pada bab sebelumnya kalian akan peroleh persamaan garis berikut.
Contoh Soal dan Pembahasannya
Tentukan persamaan garis yang melalui titik (3, 5) dan (-2, 4)!
Penyelesaian:
3. Menentukan Persamaan Garis yang Sejajar Dengan Garis Lain dan Melalui Sebuah Titik
Hal pertama yang harus dilakukan sebelum memilih persamaan garis yang sejajar dengan garis lain dan melalui sebuah titik yaitu memilih gradien garis-garis sejajar tersebut.
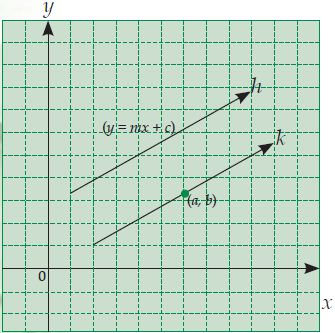
Bagaimana caranya? Perhatikan gambar di bawah ini!
Garis h mempunyai persamaan y = mx + c. Garis k sejajar garis h dan melalui titik (a,b) sehingga gradien garis k (mk) sama dengan gradien garis h (mh), yaitu m. (Ingat bahwa gradien garis yang sejajar yaitu sama).
Berdasarkan rumus sebelumnya, kita peroleh persamaan garis k yaitu y – b = m(x – a).
Jadi, persamaan garis yang sejajar dengan garis y = mx + c dan melalui titik (a, b) yaitu y – b = m(x – a).
Contoh Soal dan Pembahasannya
Tentukan persamaan garis yang melalui titik (3, 5) dan sejajar garis y = 2x – 4!
Penyelesaian:
Gradien garis y = 2x – 4 dalah m = 2. Persamaan garis yang melalui titik (3, 5) dan sejajar garis y = 2x – 4 adalah
y – 5 = 2(x – 3)
y – 5 = 2x – 6
y = 2x – 1
4. Menentukan Persamaan Garis yang Tegak Lurus Dengan Garis Lain dan Melalui Sebuah Titik
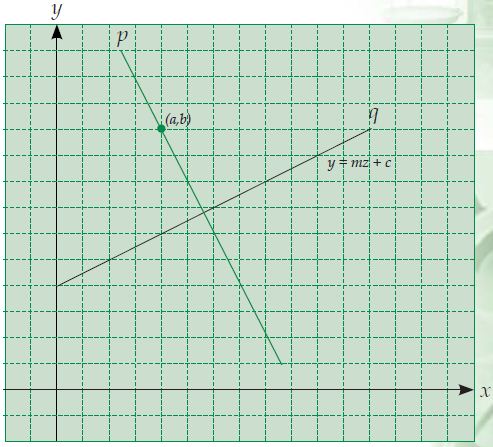
Masih ingatkah kalian bagaimana gradien dua buah garis yang saling tegak lurus menyerupai terlihat pada gambar di bawah ini?
Jika diketahui persamaan garis q yaitu y = mx + c dan garis p tegak lurus garis q dan melalui titik (a,b), dapatkah kalian mencari persamaan garis p?
Perhatikan tumpuan berikut.
Contoh Soal dan Pembahasnnya
Tentukan persamaan garis yang melalui titik (-2, 4) dan tegak lurus garis y = 2x – 4!
Penyelesaian:
Gradien garis y = 2x – 4 yaitu m = 2. Persamaan garis yang melalui titik (-2, 4) dan tegak lurus garis y = 2x – 4 adalah
Kaprikornus persamaan garis yang melalui titik (-2, 4) dan tegak lurus garis y = 2x – 4 yaitu y = –½ x + 3.
Berdasarkan tumpuan di atas dapatkah kalian memilih rumus untuk mencari persamaan garis yang melalui titik (a, b) dan tegak lurus garis y = mx + c?
Persamaan garis yang melalui titik (a, b) dan tegak lurus garis y = mx + c adalah
Demikian pembahasan lengkap perihal bagaimana cara memilih persamaan garis lurus dengan banyak sekali keadaan.
Baca juga: Rumus Persamaan Garis Lurus

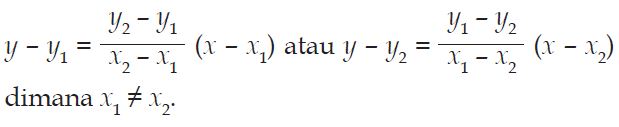




0 Response to "Cara Memilih Persamaan Garis Lurus Lengkap Dengan Pola Soal Dan Pembahasannya"
Posting Komentar