Rumus Integral Trigonometri Dan Cara Menentukannya
Rumusbilangan.com- Pengertian, Rumus Integral Trigonometri Dan Cara Menentukannya. Diantaranya integral tentu dan tak tentu beserta pola soal integral trigonometri.
Hallo sobat … Hari ini kita akan melanjutkan kembali pelajaran kita, yang mana kini kita akan mempelajari bahan tentang Rumus Integral Trigonometri Dan Cara Menentukannya.
Sub yang akan kita bahas yaitu pengertian, rumus dan bagaimana cara menentukannya atau pembahasannya.
Langsung yuk kita mulai …

Pengertian Integral Trigonometri
Integral yakni suatu bentuk operasi matematika yang menjadi kebalikan (invers) dari suatu operasi turunan dan limit dari jumlah atau suatu luas tempat tertentu.
Berdasarkan pengertian di atas, terdapat dua macam dalam integral sehingga lalu dikategorikan menjadi 2 jenis integral.
Yang pertama yaitu, integral sebagai invers/ kebalikan dari turunan yang disebut sebagai Integral Tak Tentu.
Yang kedua yaitu, integral sebagai limit dari jumlah atau suatu luas tempat tertentu yang disebut Integral Tentu.
1. Integeral Tak Tentu
Integral tak tentu yakni merupakan invers / kebalikan dari turunan. Turunan dari suatu fungsi, apabila di integralkan akan menghasilkan sebuah fungsi itu sendiri.
Perhatikanlah pola turunan-turunan dalam fungsi aljabar sebagai berikut:
- Turunan dari fungsi aljabar y yakni x3 maka yI = 3x2
- Turunan dari fungsi aljabar y yakni x3 + 8 maka yI = 3x2
- Turunan dari fungsi aljabar y yakni x3 + 17 maka yI = 3x2
- Turunan dari fungsi aljabar y yakni x3 – 6 maka yI = 3x2
Seperti yang sudah dipelajari dalam bahan turunan, variabel dalam suatu fungsi akan mengalami penurunan pangkat. Berdasarkan pola tersebut, maka sanggup diketahui bahwa ada banyak fungsi yang mempunyai hasil turunan yang sama yaitu: yI = 3x2.
Fungsi dari variabel x3 ataupun fungsi dari variabel x3 yang ditambah atau dikurang suatu bilangan, (misal contoh: +8, +17, atau -6) mempunyai turunan yang sama.
Apabila turunan tersebut dintegralkan, maka seharusnya yakni menjadi fungsi-fungsi awal sebelum diturunkan. Namun, di dalam kasus tidak diketahui fungsi awal dari suatu turunan, maka hasil integral dari turunan tersebut sanggup ditulis sebagai berikut:
Dengan nilai C sanggup berapapun. Maka notasi C ini disebut sebagai konstanta integral. Integral tak tentu dari suatu fungsi sanggup dinotasikan sebagai berikut:
Pada notasi tersebut sanggup dibaca integral terhadap x”. Notasinya disebut integran.
Secara umum integral dari fungsi f(x) ialah penjumlahan F(x) dengan C atau:
Sebab integral dan turunan berkaitan, maka rumus integral sanggup diperoleh dari rumusan penurunan. Apabila turunan:
Maka, rumus integral aljabar sanggup diperoleh:
dengan syarat .
Sebagai pola lihatlah integral aljabar fungsi-fungsi sebagai berikut:
2. Integral Tentu
Integeral Tentu yakni sebuah bentuk integeral yang variabe integrasinya mempunyai batasan.
Batasan tersebut biasanya disebut dengan sebagai batas atas dan batas bawah. Batas variabel integrasi umumnya sanggup ditulis pada belahan atas dan bawah.
Secara umum, notasi integral tentu dari suatu fungsi ini sanggup ditulis menyerupai di bawah berikut:
Rumus – Ruumus Integeral Trigonometri
Rumus integeral trigonometri yakni sebagai berikut:
Selain rumus tersebut, ada juga rumus yang lain dalam integral trigonometri yang biasa digunakan. Rumus tersebut adalah:
Demikianlah rumus – rumus integral trigonometri.
Contoh Soal dan Pembahasan
Soal 1:
Tentukanlah hasil dari ∫ (sin2 x − cos2 x) dx = …..
yakni ….
Pembahasannya:
Terdapat dua rumus trigonometri sebagai berikut:
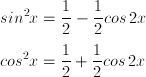
Rumus dari integral trigonometrinya adalah:
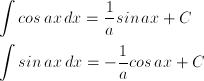
Maka, dengan demikian:
Soal 2:
Tentukanlah sebuah nilai dari o∫π/6 (sin 3x + cos 3x)dx adalah …..
Pembahasannya:
Dengan memakai rumus integral yang sama dengan soal nomor satu, maka kesudahannya sanggup ditentukan yakni sebagai berikut:
Demikianlah pembahasan bahan mengenai Rumus Integral Trigonometri Dan Cara Menentukannya. Semoga bermanfaat …
Artikel Lainnya:
Sumber aciknadzirah.blogspot.com





0 Response to "Rumus Integral Trigonometri Dan Cara Menentukannya"
Posting Komentar